Approximation des Flächeninhaltes
Nun wollen wir lernen, wir man eine krummlinig begrenzte Fläche 
annähernd berechnen kann.

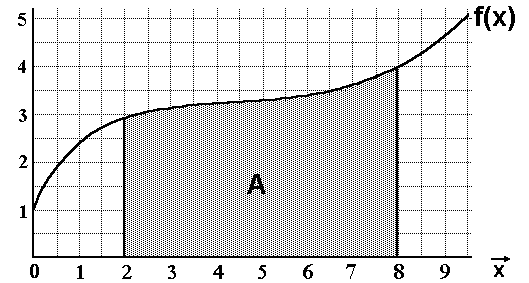
Gegeben sei eine Funktion f(x). Gesucht ist der Flächeninhalt A der grau 
eingezeichneten Fläche, also die Fläche die im :Intervall [2,8] zwischen  
der Kurve und der x-Achse liegt: 



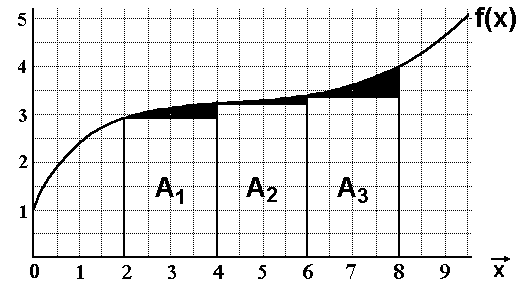
Wir teilen dazu das Intervall [2,8] in drei Teile ein von je 2cm Breite.  
In jedes Teil-Intervall zeichnen wir ein Rechteck (A1, A2 und A3), das 
so breit wie das Teil-Intervall ist. Die Höhe eines Rechtecks soll so 
hoch sein, wie der jeweils kleinste Funktionswert im Teil-Intervall:



Vergleicht man die Bilder, so stellt man fest:
Der Flächeninhalt von A1 + A2 + A3 entspricht zusammen fast dem
der grau gezeichneten Flächeninhalt von A. Lediglich die schwarz  
gezeichneten Flächen werden bei dieser Näherung nicht berücksichtigt,  
d.h. der Flächeninhalt von A1 + A2 + A3  entspricht nur ungefähr dem 
Flächeninhalt von A.  Auf der nächsten Seite werden wir diese  
Näherung verbessern. Die Summe A1 + A2 + A3 nennt man 
übrigens eine Untersumme der Fläche A. Der Name Untersumme
kommt daher, weil immer der kleinste Funktionswert in einem
Teilintervall die Höhe des Rechtecks ergeben soll.