Das
bestimmte
Integral |
 |
Erklärung
Am Ende der letzten Seite stellten wir fest, daß die
Differenz zwischen Unter- und Obersumme kleiner wird,
wenn die Differenz 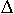 x kleiner wird. Das bedeutet aber:
Wenn wir x kleiner wird. Das bedeutet aber:
Wenn wir 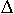 x unendlich klein werden lassen, dann wird
auch die Differenz zwischen Ober- und Untersumme
unendlich klein, und es gilt: x unendlich klein werden lassen, dann wird
auch die Differenz zwischen Ober- und Untersumme
unendlich klein, und es gilt:
Untersumme = Obersumme
(wenn 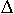 x gegen 0 geht) x gegen 0 geht) |
Andererseits kennen wir die Summen-Ungleichung:
Untersumme 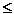 Fläche A Fläche A 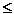 Obersumme
Faßt man beide Gleichungen zusammen, dann gilt: Obersumme
Faßt man beide Gleichungen zusammen, dann gilt:
Untersumme = Fläche A = Obersumme
(wenn 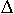 x gegen 0 geht) x gegen 0 geht)
|
Für den gemeinsamen Grenzwert zwischen
Ober- und Untersumme gibt es einen extra Namen. Man nennt diesen Grenzwert das
"bestimmte Integral":
Den gemeinsamen Grenzwert von Unter- und
Obersumme für eine unendlich kleine Zerlegung des Intervalls [a,b], nennt man das
bestimmte Integral über [a,b]. |
Das bestimmte Integral ist also gleich der gesuchten Fläche A.
Das Bild zeigt eine Fläche, die zwar nicht in unendlich viele,
jedoch symbolisch in sehr viele Rechtecke zerlegt wurde:
|
|