Erklärung
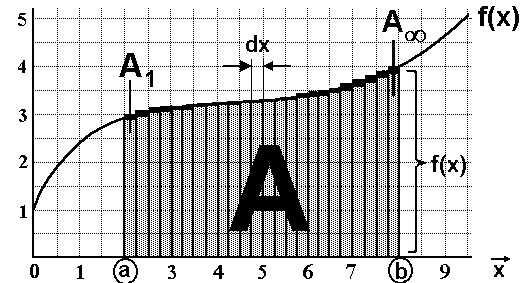
Auf der letzten Seite haben wir das bestimmte Integral 
als gemeinsamen Grenzwert von Ober- und Untersumme 
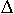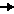für x  0 definiert. Da dieser Grenzwert offensichtlich
existiert, können wir die Limes-Schreibweise benutzen: 



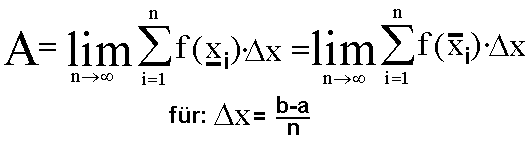Dieser Grenzwert ist so wichtig, daß es für ihn eine eigene 
Schreibweise gibt, nämlich das Integralzeichen:
     

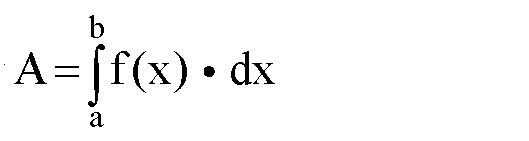
Das Integralzeichen, daß wie ein langezogenes S aussieht,
ersetzt das Summenzeichen und das Limes-Zeichen:

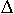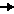    Für x  0 hat man die vereinbart, dx zu schreiben.
    dx ist also ein unendlich kleines Stück im Intervall [a,b],
    daß durch eine unendlich feine Zerteilung des Intervalls
    [a,b] entstanden ist.

    f(x) ist dann der jeweiligen Funktionswert in diesem 
    unendlich kleinen Intervall-Stück dx. 
  
Das Integralzeichen oben bedeutet also:

    Bilde die Summe aus allen Rechtecken mit den Seiten
    f(x) und dx, und zwar im Intervall [a,b]