Vertauschte
Integrations-
grenzen |
 |
Einleitung
Bis jetzt haben wir nur solche bestimmten Integrale
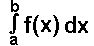 untersucht, bei denen die obere Integrations-
grenze b größer war als die untere Integrationsgrenze a: untersucht, bei denen die obere Integrations-
grenze b größer war als die untere Integrationsgrenze a:
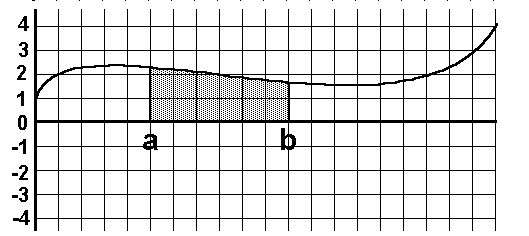 Nun geht es um bestimmte Integrale, bei denen die
obere Integrationsgrenze (b) kleiner ist als die untere (a):
Nun geht es um bestimmte Integrale, bei denen die
obere Integrationsgrenze (b) kleiner ist als die untere (a):
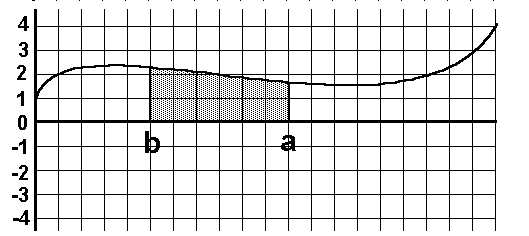
|
 |
Definition
Vertauscht man die Integrationsgrenzen des Integrals
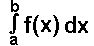 , so wechselt das Vorzeichen: , so wechselt das Vorzeichen:
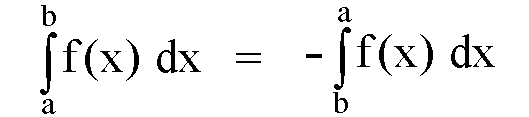
|
 |
Erklärung der Formel
Wir erinnern uns an die Definition des bestimmten Integrals:
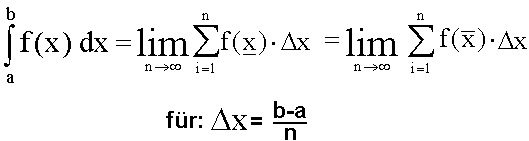 Weil (b-a) bei vertauschten Integrationsgrenzen negativ ist, ist
auch
Weil (b-a) bei vertauschten Integrationsgrenzen negativ ist, ist
auch 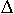 x negativ, und somit auch die Summe und das Integral. x negativ, und somit auch die Summe und das Integral.
|
|