Version: 3 ©Raddy '99

Differentialrechnung I           ZURÜCK

Tangentensteigung

Herleitung       Um eine "Formel der Tangentensteigung mt" herzuleiten, müssen wir       uns daran erinnern, daß eine Tangente eine spezielle Sekante ist,       nämlich eine Sekante bei der der Abstand zwischen P0 und P1       unendlich klein ist. Die Formel für die Sekantensteigung lautete: 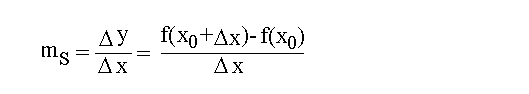             Um von der Sekantensteigung ms zur Tangentensteigung mt zu        gelangen, müssen wir in der Formel der Sekantensteigung die        Eigenschaft der Tangente dazufügen, daß der Abstand zwischen        P0 und P1 endlich klein ist. Dazu benutzen die Limes-Schreibweise,        die wir im Kapitel Grenzwerte I kennengelernt haben: 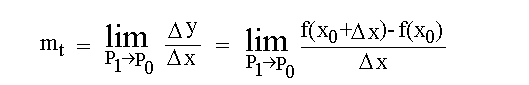             Wenn die Punkte P0 und P1 unendlich nahe aneinanderliegen, dann        liegen auch die Koordinaten x0 und x1 unendlich nah aneinander.        Somit nähert sich 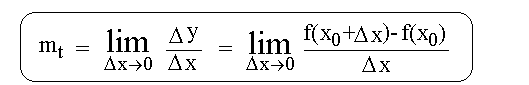x dem Wert 0 und wir dürfen schreiben:       Bedeutung der Formel       Auf der letzten Formel baut die gesammte Differentialrechnung auf:       Weil die Tangentensteigung im Punkt P0 die gleich Steigung       hat wie die Kurve im Punkt P0 (Erkenntnis der vorigen Seite),       kann man mit der Formel "Tangentensteigung" die Steigung       einer beliebigen Kurve berechnen!       Mit dieser Formel haben wir also das Gundproblem der       Differentialrechnung zumindest prinzipiell gelöst: Das       Berechnen der Steigung einer Kurve in einem beliebigen Punkt P0.       Wie das bei einer konkreten Funktion (z.B. y=x²) funktioniert,       zeigen wir im nächsten Kapitel.