Version: 3 ©Raddy '99

Differentialrechnung II           ZURÜCK

Ableitung und Differential- quotient

Ableitung und Differentialquotient       Bis jetzt haben sind wir bis zu diesem Punkt gekommen:       Wir haben eine Formel entwicket, mit der man die Kurven- bzw.       Tangentensteigung in einem beliebigen Punkt x0 berechnen kann.       Eine Kurve hat aber nicht immer nur eine rein geometrische       Bedeutung. Oft beschreibt man mit einer Kurve die Abhängigkeit       zweier (z.B. physikalischer) Größen.       Als Beispiel diene eine Kurve, die eine Geschwindigkeit-Zeit-       Funktion wiedergibt. Im Bild sehen wir eine Kurve, die den       Beschleunigungsvorgang eines Auto von 0 auf 200km/h darstellt: 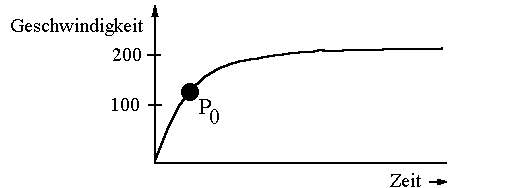            Der Kurvensteigung (im Punkt P0) entspricht dann physikalisch       die Zunahme der Geschwindigkeit in P0, also die Beschleunigung.       Wenn wir also die Kurvensteigung berechnen, berechnen wir       in Wirklichkeit die physikalische Größe "Beschleunigung".       Deshalb ist es nötig, dem Begriff Kurvensteigung einen       allgemeineren Namen zu geben. Anstatt Kurvensteigung in P0       sagt man Ableitung in P0 oder Differentialquotient in P0. Schreib- und Sprechweisen       Wie gesagt wollen wir ab jetzt nicht mehr von der Tangentensteigung       sprechen, sondern von der Ableitung (bzw.dem Differentialquotient).       Folglich dürfen wir auch nicht mehr mt schreiben, sondern wir       schreiben ab jetzt (für die Ableitung bzw. Differentialquotienten): 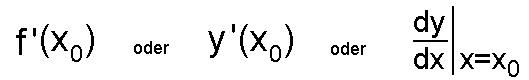            Und so wird die Ableitung (der Differentialquotient) ausgesprochen: