Fakultäten  
Beweis der Formel:



 
a-absatz.pcx (280 Byte) Hinweis: Beweis auch als Video verfügbar
Der Beweis ist auch in Form von Youtube-Videos verfügbar: Video
    
a-absatz.pcx (280 Byte) Beweis
Beachte: In den beiden linken Spalten findet man den allgemeinen Beweis, in den beiden rechten ein Beispiel.
Allgemein Ausführlich   Beispiel Ausführlich
Die Doppelfakultät (2n–1) bzw. das Beispiel 7!! sollen durch einfache Fakultäten ausgedrückt werden:
 
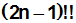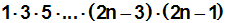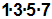Wir erweitern mit einer Doppelfaktultät, deren Argument um 1 größer ist als das gegebene Argument:
Wir erweitern mit:
 (2n)!!		 Wir erweitern also mit:
2·4·6·...·(2n–2)·(2n)		   Wir erweitern
mit: 8!! 		Wir erweitern also
mit: 2·4·6·8
 
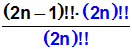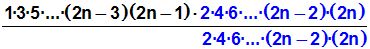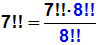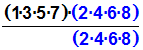Dadurch wird die Doppelfakultät im Zähler zu einer einfachen Fakultät.
Man erkennt es, wenn man die Faktoren im Zähler umordnet:
 
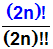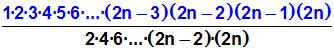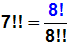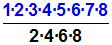Im Nenner können wir die Umrechnungsformel für die "Doppelfakultät einer geraden Zahl" anwenden,
die wir im vorigen Abschnitt dieses Kapitels kennengelernt haben: (2n)!!=2n·n!
---   ---

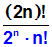Unser Ziel ist erreicht: Dies ist die Formel, die wir beweisen wollten.