Die Anwendung einer
injektiven Funktion
ist eine
Äquivalenzumformung |
 |
Satz |
| |
Macht man beide
Seiten einer Gleichung zum Argument einer injektiven Funktion,
dann ist dies eine Äquivalenzumformung,
d.h. die neue
Gleichung hat die
gleichen
Lösungen wie die ursprüngliche Gleichung.
Die injektive Funktion muss natürlich für alle
Werte
definiert sein, welche
die beiden Seiten der Funktion annehmen
können. |
|
| |
|
 |
Was ist eine injektive
Funktion? |
|
Was ein injektive Funktion ist, haben wir im Kurs
Funktionen ausgiebig erklärt:
Es sind
Funktionen bei denen jeder Funktionswert höchstens einmal auftritt.
Beispielsweise (aber nicht nur) sind alle
"streng monotonen Funktionen"
injektiv,
also z.B. ungerade Potenzfunktionen, die Exponentialfunktion, die
Wurzelfunktion,
die Logarithmusfunktion usw.
|
 |
Beispiel |
|
Wir haben gerade gesagt, dass es eine
Äquivalenzumformung darstellt, wenn wir
beide Seiten einer Gleichung zum Argument einer injektiven Funktion
machen.
Gegeben ist die Gleichung:
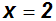
Wir machen nun beide Seiten
der Gleichung zum Argument der Kubikfunktion. Dies ist
eine Äquivalenzumformung, denn erstens ist die Kubikfunktion injektiv (da
streng monton
steigend),
und zweitens hat die Funktion einen ausreichend großen
Definitionsbereich D,
sodass kein undefinierter Ausdruck entstehen kann:
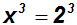
Wir vereinfachen:
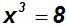
Überprüfen wir nun, ob es sich wirklich um eine
Äquivalenzumformung
handelt:
Die erste Gleichung hat die Lösung 2. Diese
Zahl ist auch die einzige
Lösung
der zweiten Gleichung, was man durch Einsetzen der
Zahl 2
in die zweite Gleichung
überprüfen kann. Somit handelt es sich um
eine
Äquivalenzumformung.
|
|