UND-Funktion
Seite 1 von 3

Vorbemerkung
       In diesem Kapitel werden wir drei der am häufigsten vorkommenden
       sogenannten Wahrheitsfunktionen kennenlernen: Die UND-Funktion, 
       die ODER-Funktion und die EXKLUSIV-ODER-Funktion. 
       Als erstes werden wir die sogenannte UND-Funktion 
       (auch: UND-Verknüpfung genannt) kennenlernen.
 
       Zuvor jedoch wollen wir kurze den Begriff "Funktion zweier
       unabhängiger Variablen" wiederholen, das die Wahrheits-
       funktionen zu dieser Sorte von Funktionen gehören!
 
Wiederholung
      Funktionen zweier unabhängiger Variablen" sind Funktionen, in 
      denen drei Variablen vorkommen, von denen zwei Variablen (x,y) 
      unabhängig sind, und eine Variable (z) abhängig ist. Beispiele:
 
               z= x+y        oder     z=x-y        oder     z=x·y
 
      Als Anwendungsbeispiel für "Funktionen zweier Veränderlicher"
      hatten wir die Funktion "Monatslohn" gewählt: 
 
             X: Anzahl der (in diesem Monat) gearbeiteten Stunden 
             Y: Stundenlohn des Arbeiters
             Z: Monatslohn 
 
      Hier war die Variable Z die (von X und Y) abhängige Variable.
 
      Wir hatten dann zwei Darstellungsformen für "Funktionen zweier
      unabhängiger Variablen" kennengelernt:
 
      Œ Räumliches Koordinatensystem
         
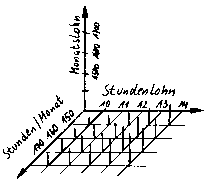       Tabelle
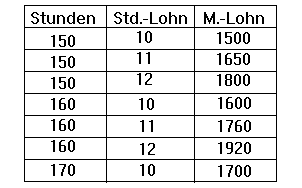