|
Um eine Polynomungleichung zu lösen, kann man auch das Tabellenverfahren
verwenden, dass wir in diesem Kapitel vorstellen werden. Wir erklären
das
Tabellenverfahren zuerst für den Sonderfall, dass die Polynomungleichung
als
Produkt vorliegt, und zwar in Linearfaktoren zerlegt ist.
Dies ist sinnvoll, weil der
allgemeine Fall
(Polynomungleichung liegt nicht als Produkt vor)
auf den Sonderfall
zurückgeführt werden kann.
|
|
Schritt 1:
Gegeben sei also eine Polynomungleichung in Produktform:
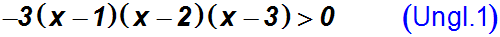
Schritt 2:
Wir teilen die Ungleichung durch den konstanten Faktor –3. Beachte:
Weil –3 eine negative Zahl ist, ändert das Ungleichheitszeichen
seine Richtung:
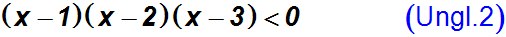
Schritt 3:
Jetzt betrachten den Term (das Produkt) auf der linken Seite der
Ungleichung und
fragen uns, in welchen Intervallen er sein Vorzeichen ändert. Dies ist
genau dann der Fall,
wenn einer der Faktoren sein Vorzeichen ändert, also wenn x=1, x=2 oder
x=3.
In den Intervallen, die entweder vor, zwischen und nach diesen Stellen
liegen,
ändert sich das Vorzeichen des Produktes natürlich nicht.
Wir tragen diese Intervalle,
in denen sich das Vorzeichen des Produktes nicht ändert, in eine Tabelle
ein:
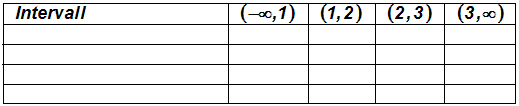
Nebenbei bemerkt: An den Stellen x=1, x=2 und x=3 ist das Produkt gleich
Null, d.h.
die Ungleichung ist dort falsch. Daher werden wir diese drei Stellen
nicht mehr beachten.
Schritt 4:
Nun bestimmen wir die Vorzeichen der einzelnen Faktoren aus Ungleichung
2.
Dazu tragen wir zunächst die Faktoren in die Tabelle ein:

Als Beispiel erklären wir, welches Vorzeichen der Faktor (x–1) im
Intervall (–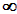 ,1) hat, ,1) hat,
und tragen das Ergebnis in die Tabelle ein: Setzen wir in den Faktor
(x–1) eine Zahl aus
dem Intervall (– ,1)
ein, dann wird der Faktor negativ. Wir tragen
daher ein "Minus" ein: ,1)
ein, dann wird der Faktor negativ. Wir tragen
daher ein "Minus" ein:
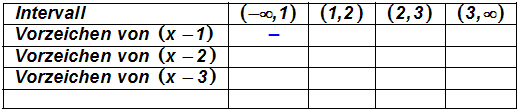
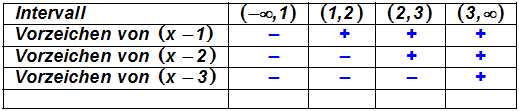
Die restlichen Vorzeichen ergeben sich genauso einfach:
Schritt 5:
Jetzt ermitteln wir das Vorzeichen der linken Seite von Ungleichung 2,
also das Vorzeichen
des Terms (x–1)·(x–2)·(x–3), und schreiben den Term dazu in die letzte
Zeile:
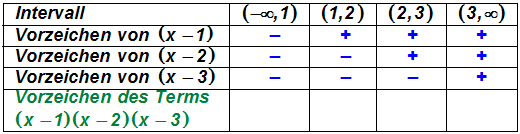
Als Beispiel erklären wir, welches Vorzeichen der Term (x–1)·(x–2)·(x–3)
im Intervall
(–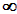 ,1) hat. Das Vorzeichen
ergibt sich dabei aus den Vorzeichen der einzelnen
Faktoren ,1) hat. Das Vorzeichen
ergibt sich dabei aus den Vorzeichen der einzelnen
Faktoren
im Intervall (–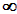 ,1),
die wir zuvor bestimmt haben. Im Intervall (– ,1),
die wir zuvor bestimmt haben. Im Intervall (–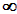 ,1)
sind alle ,1)
sind alle
Faktoren negativ (minus). Nun gilt aber die Vorzeichenregel der
Multiplikation, d.h. es gilt:
Minus · Minus ·
Minus ergibt Minus
Also hat der gesamte Term (x–1)·(x–2)·(x–3) ein negatives Vorzeichen
im Intervall (–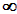 ,1). ,1).
Wir
tragen das Vorzeichen (das Minus) in die Tabelle ein (in grüner Farbe):
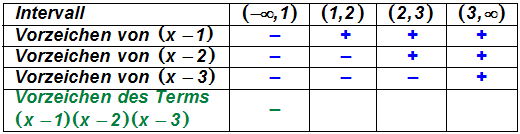
Die restlichen Vorzeichen des Terms (x–1)·(x–2)·(x–3) ergeben sich
ebenso einfach:
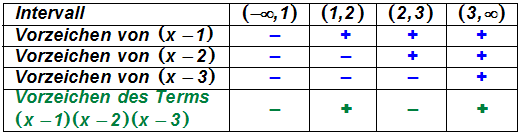
Schritt 6:
Nun kennen wir das Vorzeichen von (x–1)·(x–2)·(x–3) in allen
Intervallen, und können
daher die Ungleichung (x–1)·(x–2)·(x–3)<0 lösen, d.h. die Ungleichung 2.
Laut Tabelle ist der Term (x–1)·(x–2)·(x–3) in den beiden Intervallen (– ,1)
und (2,3) ,1)
und (2,3)
kleiner Null und somit ist Ungleichung 2, d.h. die Ungleichung
(x–1)·(x–2)·(x–3)<0 dort wahr.
Die Lösungsmenge der Ungleichung 2 ist somit die Vereinigungsmenge:
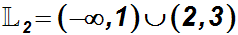
Weil Ungleichung 2 und Ungleichung 1 (gegebene Ungleichung) äquivalent
sind,
lautet die Lösungsmenge der gegebenen Ungleichung ebenfalls:
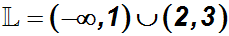
|