Absolut konvergente
Reihen sind auch
immer konvergent
im "normalen" Sinn. |
 |
Satz |
|
| Eine absolut konvergente Reihe ist auch
konvergent. |
|
 |
Anwendung |
|
Von der folgenen Reihe wissen wir, dass sie konvergiert,
denn sie ist eine geometrische Reihe mit |q|<1:
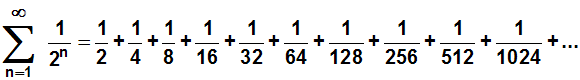
Nun sei eine weitere Reihe gegeben. Sie ist gleich der vorigen,
jedoch ist jedes dritte Glied negativ:
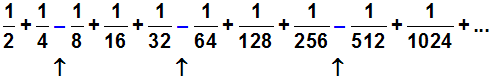
Stellt sich nun die Frage, ob auch diese Reihe konvergiert, so müssen
wir nur
die obigen Satz anwenden: Da sie absolut konvergent ist, ist sie auch
konvergent.
|
|
|
|