 |
Die Formel, die wir beweisen
wollen |
|
Hier nochmal zur Erinnerung die Formeln, die wir beweisen wollen:
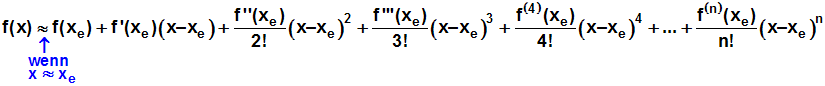
Oder in der Schreibweise mit dem Summenzeichen:
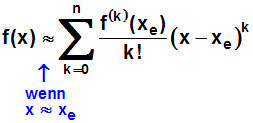
|
 |
Herleitung Schritt 1 |
|
Wir wollen eine Funktion durch ein Polynom approximieren,
sodass Funktion und Polynom an der Stelle xe gut
übereinstimmen.
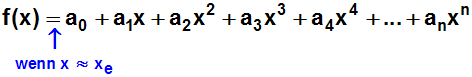
Weil Funktion und Polynom an der Stelle xe
genau übereinstimmen sollen,
ersetzen daher x durch xe und setzen dann Funktion und
Polynom gleich.
Dann versuchen wir, die Koeffizienten a0 , a1 , a2
, ... zu ermitteln:
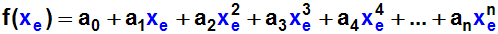
Nun haben wir ein Problem: Wir haben eine Gleichung mit
fünf Unbekannten,
nämlich a0 , a1 , a2 , a3
und a4. Die Ermittlung des Koeffizienten a0
ist also gescheitert!
Bei der Entwicklungsstelle x=0 trat dieses Problem nicht auf, weil beim
Einsetzen
von x=0 die letzten Terme alle zu Null werden. Aber vielleicht gibt es
ja einen Trick,
damit die letzten Terme zu Null werden, wenn wir xe
einsetzen? Ja, es gibt so einen Trick!
|
 |
Herleitung Schritt 2 |
|
Der Trick ist, die Funktion f(x) durch eine neues Polynom zu approximieren,
bei der x durch x–xe ersetzt wurde. Das es sich
tatsächlich um ein Polynom handelt,
merkt man übrigens schnell, wenn man die Klammern ausmultipliziert:
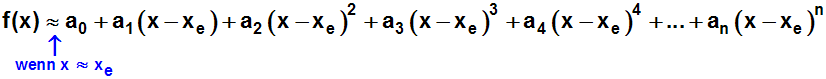
Wie bereits erwähnt, sollen Funktion und Polynom an der Stelle xe
gleich sein,
damit zumindest an der Stelle xe die Approximation absolut
genau ist,
und daher müssen wir Funktion und Polynom an der Stelle x=xe gleichsetzen:
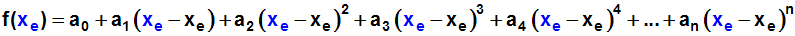
Weil alle Klammern zu Null werden, hat der Trick funktioniert: Wir haben
den Koeffizienten a0 gefunden: a0 = f(xe).
Wir leiten Funktion und Polynom ab, und setzen die Ableitungen an der
Stelle xe gleich,
denn wie schon öfter erwähnt,
sollen auch die "Ableitung der Funktion" mit der "Ableitung
des Polynoms" an der Stelle x=xe gleich sein,
damit die Approximation an der Stelle xe möglichst gut ist:
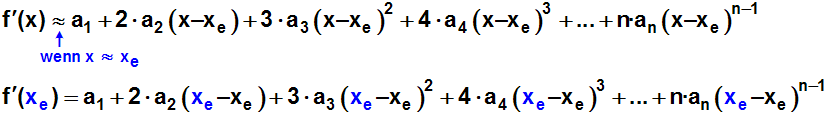
Weil wieder alle Klammern zu Null werden, können wir a1
ablesen: a1=f '(xe).
Dieser Schritt wiederholt sich jetzt immer wieder, denn
auch die höheren Ableitungen
der Funktion und des Polynoms sollen an der Stelle xe gleich
sein. Wir leiten daher die Funktion
und das Polynom nochmal ab und setzen sie an der Entwicklungsstelle x=xe
gleich:
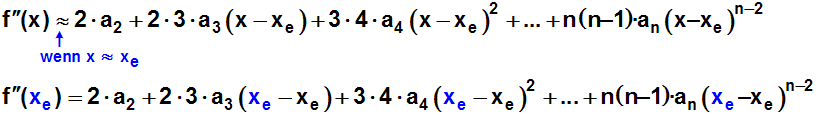
Weil wieder alle Klammern (die xe–xe
enthalten) zu Null werden, erhalten wir:
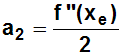
Und nochmal beide Seiten ableiten und an der Stelle x=xe
gleichsetzen:
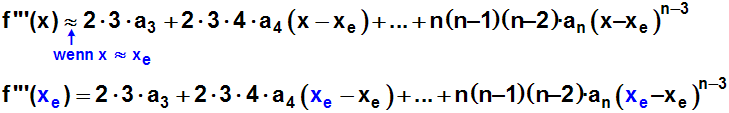
Weil wieder alle Klammern (die xe–xe
enthalten) zu Null werden,
erhalten wir: 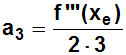
Und nochmal beide Seiten ableiten und an der Stelle x=xe
gleichsetzen:
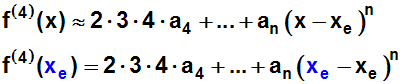
Weil wieder alle Klammern (die xe–xe
enthalten) zu Null werden, erhalten wir:
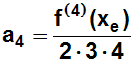
Schließlich bilden wir die n-te Ableitung, und weil
wieder die Ableitungen (von Funktion und Polynom)
an der Stelle xe gleich sein sollen, setzen wir die
Ableitungen an der Stelle xe gleich:
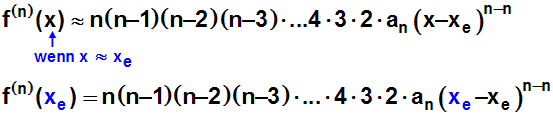
Weil die Klammer (die xe–xe enthält) zu Null wird, erhalten wir:
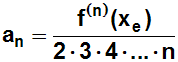
|
 |
Herleitung Schritt 3 |
|
Der ursprüngliche Ansatz für die Taylorreihe (siehe
Schritt 2) lautete:
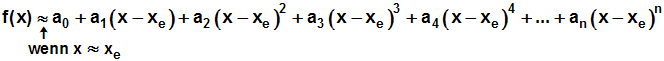
Die ermittelten Koeffizienten a0 , a1 , a2
, ..., an
setzen wir in diese Formel ein:
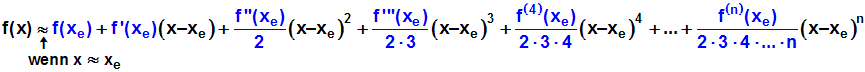
Als Vorbereitung des nächsten Schritts (Fakultäts-Schreibweise
einführen) dividieren wir alle Terme durch 1.
Dies ist erlaubt, denn eine Division durch 1 ändert einen Term
bekanntlich nicht. Wir erhalten:
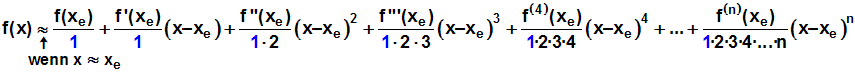
Um die Darstellung zu vereinfachen, benutzen wir wieder die
sogenannte Fakultät-Schreibweise:
Produkte wie 1·2·3·4 werden geschrieben als 4! (sprich: 4
Fakultät). Oder allgemein gesagt: 1·2·3·4·...·n = n!
Beachte, dass außerdem bei der Definition der Fakultät festgelegt wurde,
dass 0!=1, 1!=1. Wir erhalten:
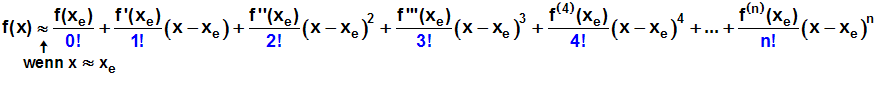
Wenn wir jetzt noch festlegen, dass man unter der nullten Ableitung einer Funktion
f die Funktion selbst versteht,
dass also gilt: f(x)=f (0)(x) ,
dann kann man sich das Bildungsgesetzt für die Glieder der Taylorreihe leicht
merken:
Die Ordnung
der Ableitung ist identisch mit dem Argument der Fakultät
und dem
Exponenten der Klammer (x–xe).
Wir können daher auch die verkürzte Schreibweise mit dem Summenzeichen wählen:
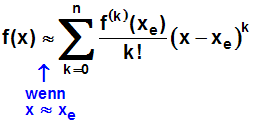
Es hat sich aber eingebürgert, dass im Nenner des ersten und zweiten
Gliedes 0!=1 bzw. 1!=1 weggelassen wird. Wir erhalten die gesuchte
Formel:
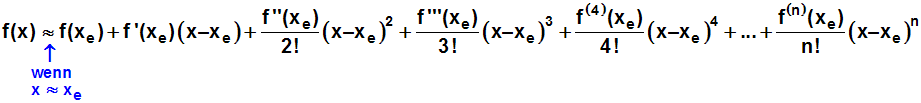 |
| |
|