Funktionen mit
Punktsymmetrie
zum Ursprung
(ungerade Funktionen) |
 |
Erklärung |
|
Man nennt eine Funktion punktsymmetrisch zum
Ursprung (oder ungerade),
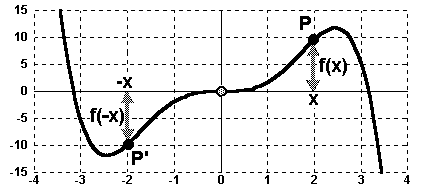
wenn jeder negative x-Wert (-x) den gleichen Funktionswert f(-x) hat, wie
der zugehörige positive x-Wert, jedoch das umgekehrte Vorzeichen:
f(–x) = –f(x)
Für den Graphen bedeutet dies: Spiegelt man einen
beliebigen Punkt P
des Graphen am Ursprung, so erhält man einen Punkt P', der ebenfalls
zum Funktionsgraphen gehört.
Man nennt solche Funktionen mit Punktsymmetrie zum Ursprung
meist
ungerade Funktionen. Diese Gewohnheit beruht darauf, dass
Potenzfunktionen
mit ungeraden Exponenten stets punktsymmetrisch zum Ursprung sind.
|
 |
Beispiel |
|
Wie bereits gesagt, sind alle Potenzfunktionen mit ungeraden Exponenten
auch punktsymmetrisch zum Ursprung:
f(x) = x3
|
 |
Beispiel |
|
Die Sinusfunktion ist ebenfalls eine ungerade
Funktion, also punktsymmetrisch
zum Ursprung:
f(x) = sin(x)
|
|
|
|