Version: Test
©Raddy 2000

Trigonometrie V                                       ZURÜCK
Beweis des
Sinussatz		 a-absatz.pcx (280 Byte)Der Beweis des Sinussatzes
       Auf dieser Seite wollen wir den Sinussatz beweisen.
       Der Beweis des Sinussatz ist sehr einfach aufgebaut.

       Gegeben sei das folgende Dreieck: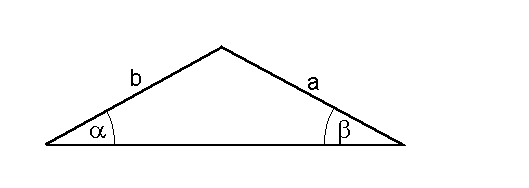
       tr5s2p2.pcx (2805 Byte)
       In dieses Dreieck zeichnen wir die Höhe hc ein.
       Dadurch entstehen zwei rechwinklige Dreiecke.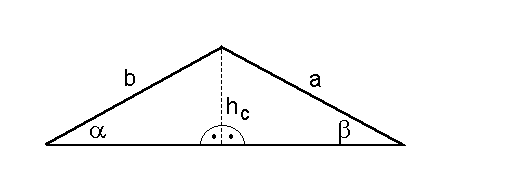
       tr5s3p2.pcx (2733 Byte)
       Für die beiden rechtwinkligen Dreiecke gelten die
       folgenden Beziehungen: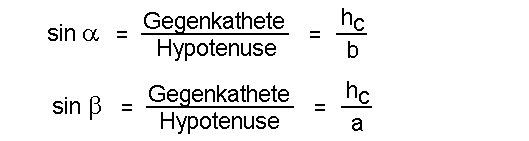
           tr5s2p3.pcx (1309 Byte)
       Wir stellen beide Gleichungen nach hc um:
         tr5s2p4.pcx (2812 Byte)
       Dadurch können wir die beiden Gleichungen gleichsetzen: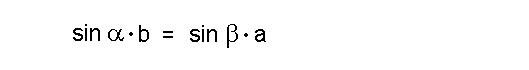
       tr5s3p5.pcx (1109 Byte)
       Nun müssen wir die Gleichung nur noch umformen, und
       erhalten den Sinussatz in der uns bekannten Form:
       tr5s3p6.pcx (1078 Byte)