Version: Test ©Raddy 2000	Inhalt zu: Vektoralgebra III ZURÜCK
Info-Seite	Vorkenntnisse: ... Themen: ... Infos: www.mathematik.net
Linearkombination	Gegeben sei eine Menge {v, w, ...} von Vektoren . k₁, k₂, ... seien reelle Zahlen. Dann nennt man jeden Vektor a der Form a = k₁·v + k₂·w + ... eine Linearkombination der Vektoren v, w, ...
Nullsummen	Eine Linearkombination k₁·v+k₂·w+ ... kann gleich dem Nullvektor sein. Die Linearkombination nennt man in diesem Fall eine Nullsumme, die grafisch einer geschlossenen Vektorkette entspricht.
Nichtriviale Nullsummen	Ein Spezialfall ist die triviale Nullsumme, bei der alle Koeffizienten k₁,k₂, ... gleich 0 sind: 0 = 0·v + 0·w + 0·x + ...
Lineare Abhängigkeit	Gegeben sei eine Menge {v, w, ...} aus Vektoren. Findet man unter den Linearkombinationen der Menge {v, w, ...} außer der "trivalen Nullsumme" auch eine "nichttriviale Nullsumme", so nennt man die Menge {v, w, ...} linear abhängig.
Lineare Abhängigkeit zweier Vektoren	Zwei Vektoren sind genau dann linear abhängig, wenn sie kollinear sind.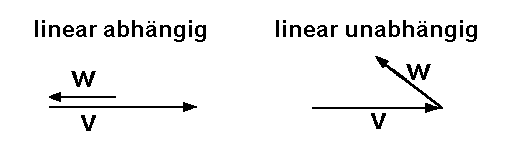
Komplanarität	Drei Vektoren nennt man komplanar, wenn sie alle in einer Ebene liegen.
Lineare Abhängigkeit dreier Vektoren	Drei Vektoren sind genau dann linear abhängig, wenn sie komplanar sind.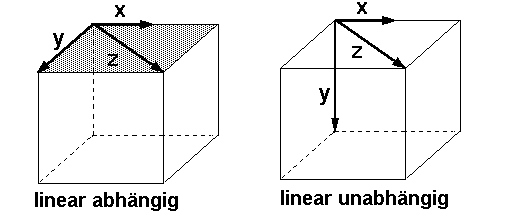
Beweis dazu	Aus drei Vektoren in einer Ebene kann man ein Dreieck konstruieren, daß eine geschlossene Vektorkette darstellt .... daraus folgt: es gibt eine nichttriviale Nullsumme ... daraus folgt: die Vektoren sind linear abhängig
Lin. Abhängigkeit bei 4 Vektoren	Vier Vektoren im Raum (oder Ebene) sind immer linear abhängig.
Beweis	Der Beweis dazu ...
Eigenschaft linear abhängiger Vektoren	Ist eine Menge {v, w, ...} aus Vektoren linear abhängig, so gibt es mindestens einen Vektor, der sich als Linearkombination der restlichen Vektoren ausdrücken läßt.
Beweis	Der Beweis dazu ...