Gegeben sei eine Menge {v, w, ...}
aus Vektoren.
Findet man unter den Linearkombinationen der Menge
{v, w, ...}
außer der trivalen Nullsumme auch eine nichttriviale Nullsumme,
so nennt man die Menge
{v, w, ...} linear abhängig.
Findet man unter den Linearkombinationen von {v, w, ...}
nur die "triviale Nullsumme", so nennt man die Menge
{v, w, ...} linear unabhängig.
Beispiel: Lineare Abhängigkeit
Gegeben seien die zwei Vektoren v und w:
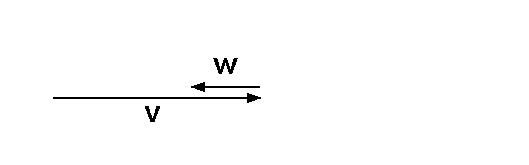Wie man sieht, kann man mit Ihnen nicht nur eine triviale Nullsumme bilden,
sondern auch eine nichttriviale Nullsumme bilden:
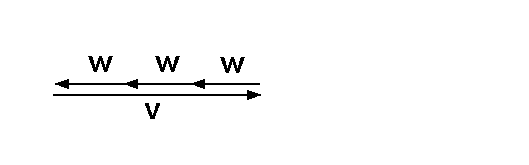Somit sind die beiden Vektoren v und w linear abhängig.
Beispiel: Lineare Unabhängigkeit
Gegeben seien die zwei Vektoren v und w:
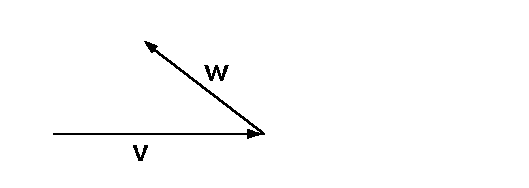Wie man sieht kann man mit Ihnen keine Nullsumme bilden,
(außer der trivialen Nullsumme, die man ja immer bilden kann).
Somit sind die beiden Vektoren v und w linear unabhängig.
Definition
Wie man sieht, kann man mit Ihnen nicht nur eine triviale Nullsumme bilden,
sondern auch eine nichttriviale Nullsumme bilden:
Somit sind die beiden Vektoren v und w linear abhängig.
Wie man sieht kann man mit Ihnen keine Nullsumme bilden,
(außer der trivialen Nullsumme, die man ja immer bilden kann).
Somit sind die beiden Vektoren v und w linear unabhängig.