Version: Test
©Raddy 2000

Vektoralgebra III                                     ZURÜCK

Beispiele für lineare Abhängigkeit
       Nun wollen wir untersuchen, wann zwei Vektoren linear
       abhängig sind. Auf der vorigen Seite hatten wir die beiden
       Vektoren v und w betrachtet:
       
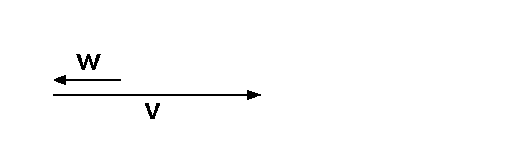       Wir nannten sie linear abhängig, weil man mit ihnen eine 
       nichtriviale Nullsumme bilden kann:  0 = 1·v + 3·w
        
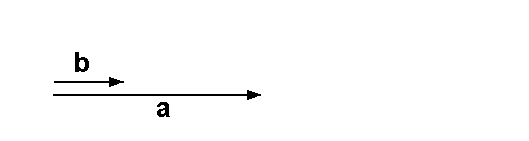
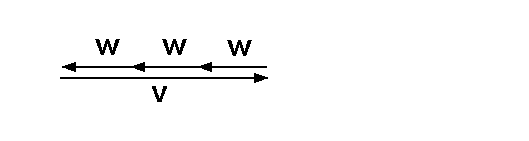       Nun betrachten wir zwei andere Vektoren, nämlich a und b.
       Im Gegensatz zu v und w haben a und b die gleiche Richtung:
       
       Auch a und b sind linear abhängig, denn man kann folgende
       nichttriviale Nullsumme bilden:  0 = 1·a - 3b
       
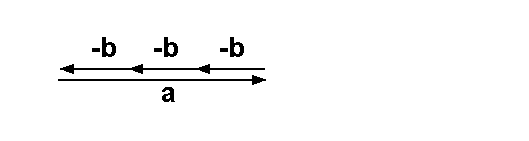       Anscheinend sind zwei Vektoren immer dann linear abhängig, 
       wenn sie die gleiche oder entgegengesetzte Richtungen haben,
       mit anderen Worten: Wenn die Vektoren parallel verlaufen.
       Man nennt parallel verlaufende Vektoren auch kollineare
       Vektoren, und somit gilt:

Lineare Abhängigkeit zweier Vektoren