Lineare
Abhängigkeit
bei 3 Vektoren |
 Lineare Abhängigkeit bei 3 Vektoren
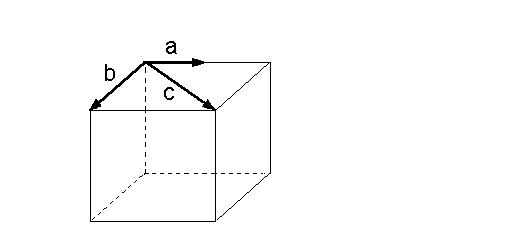
Nun wollen wir überlegen, in welchen Fällen drei Vektoren
linear abhängig sind. Gegeben seien drei Vektoren die in
derselben Ebene liegen (komplanare Vektoren): Lineare Abhängigkeit bei 3 Vektoren
Nun wollen wir überlegen, in welchen Fällen drei Vektoren
linear abhängig sind. Gegeben seien drei Vektoren die in
derselben Ebene liegen (komplanare Vektoren):
 Nun kann man sich überlegen, daß die drei Vektoren unseres
Beispiels linear abhängig sind, denn man kann mit ihnen
die nichttriviale Nullsumme 0=2a+1b-1c bilden:
Nun kann man sich überlegen, daß die drei Vektoren unseres
Beispiels linear abhängig sind, denn man kann mit ihnen
die nichttriviale Nullsumme 0=2a+1b-1c bilden:
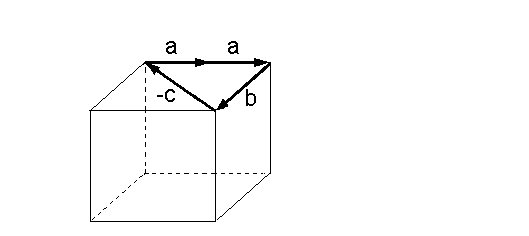 Anscheinend sind komplanare Vektoren immer linear abhängig.
Anscheinend sind komplanare Vektoren immer linear abhängig.
 Lineare Unabhängigkeit bei 3 Vektoren
Nun betrachten wir drei nicht komplanare Vektoren: Lineare Unabhängigkeit bei 3 Vektoren
Nun betrachten wir drei nicht komplanare Vektoren:
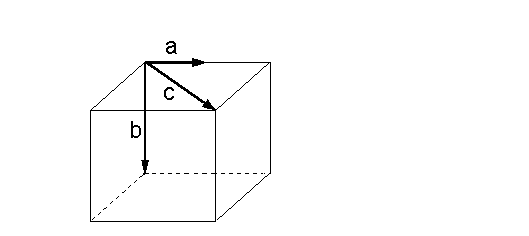 Anscheinend kann man mit nicht komplanaren Vektoren keine
nichttriviale Nullsumme bilden, und somit sind sie linear
unabhängig. Wir halten fest:
Nicht komplanare Vektoren sind linear unabhängig.
Anscheinend kann man mit nicht komplanaren Vektoren keine
nichttriviale Nullsumme bilden, und somit sind sie linear
unabhängig. Wir halten fest:
Nicht komplanare Vektoren sind linear unabhängig.
|