Wurzelgleichungen mit zwei Quadratwurzeln und Absolutglied Wurzel isolieren: Auf beiden Seiten addieren: Gleichung potenzieren: Nun beide Seiten quadrieren. Achtung: Auf der linken Seite nicht nur die Wurzel quadrieren (häufiger Fehler) sondern die gesamte linke Seite: Vereinfachen: Auf der rechten Seite heben sich Radizieren und Potenzieren auf. Die linke Seite ist ein 2.Binom, schreibe es als Summe: 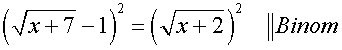Wurzel isolieren: Nachdem wir auf der linken Seite das Binom als Summe geschrieben haben, fangen wir an, die verbleibende Wurzel zu isolieren: Dazu subtrahieren wir auf beiden Seiten x und 8: Wurzel isolieren: Durch Division mit –2 wird die Wurzel vollständig isoliert Gleichung nochmal potenzieren: Um die isolierte Wurzel zu beseitigen müssen wir quadrieren: Umformen: Auf der linken Seite heben sich Quadrieren und Potenzieren auf. Nun 7 auf beiden Seiten subtrahieren: Ergebnis: Das Ergebnis ist x=2 Probe: In die ursprüngliche Gleichung setzen wir das Ergebnis x=2 ein. Die Probe führt zu einer wahren Aussage, und damit ist x=2 wirkliche eine Lösung der Wurzelgleichung.
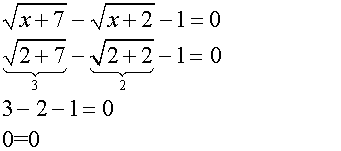