Erklärung
Wir haben nun zwei Formeln für die Fläche S kennengelernt:

 Wir setzen nun Formel 1 in Formel 2 ein: 


Wir teilen diese Ungleichung durch 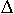x: 


Der mittlere Term stellt einen Differenzenquotienten dar, wie
wir ihm im Lehrgang Differentialrechnung kennen gelernt haben.

Nun führen wir den Grenzwertübergang 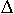x 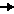 dx  durch: 
Dadurch wird f() = f()  und der mittlere Term geht vom
Differenzenquotienten in den Differentialquotienten über:

f(x) = S'(x)

Diese Formel wird oft als der 1.Hauptsatz der Differential- 
und Integralrechnung bezeichnet, einer Vorstufe des wichtigen
2.Hauptsatzes.