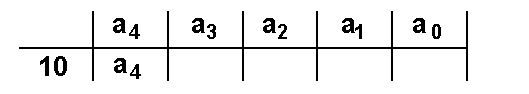Nun wollen wir erklären, warum das Horner-Schema funktioniert.
Als Beispiel betrachten wir das Polynom: 

            a4x4 + a3x3 + a2x2 + a1x  + a0

und wollen den Funktionswert an einer beliebigen Stelle berechnen, 
z.B. an der Stelle x=10.

Zuerst klammern x aus allen Summanden aus, die x enthalten:

       (a4x3 + a3x2 +  a2x + a1)x  + a0

Aus den ersten drei Termen (in der Klammer) können wir nochmal x ausklammern:

       ((a4x2 + a3x +  a2)x + a1)x  + a0

Dieses Vorgehen wiederholen wir, bis x nur noch in der
1. Potenz vorkommt:

       (((a4x + a3)x +  a2)x + a1)x  + a0

Da wir den Funktionswert an der Stelle x=10 berechnen wollten,
müssen wir für x die Zahl 10 einsetzen:

       (((a4·10 + a3)·10 + a2)·10 + a1)·10  + a0

Nun sind wir am Ende der Zerlegung. 
Überlegen wir, was diese Rechnenvorschrift vorschreibt:

         Man nimmt dem höchsten Koeffizienten (hier: a4) und
         multipliziert ihn mit 10, addiert den nächst kleineren
         Koeffizienten (hier: a3), multipliziert wieder mit 10,
         addiert wieder den nächst kleineren Koeffizenten ....

Genau dieses Verfahren ist aber das Horner-Schema, was man sich
an der nachfolgenden Tabelle nochmals verdeutlichen kann: