Bei der "Division ganzer Zahlen" hatten wir festgestellt,
daß die Division ohne Rest aufgehen kann:
175 : 7 = 25
Im allgemeinen geht die Division ganzer Zahlen aber nicht
auf, d.h. das Ergebnis ist eine ganze Zahl plus einem
(echten) Bruch:
 Bei der Division vom Polynomen gibt es auch diese zwei Fälle.
Unser erstes Beispiel einer Polynomdivisionen ging glatt auf:
(x2 -1) : (x+1) = (x-1)
Meist jedoch ergibt eine Polynomdivision ein Polynom q(x)
plus einem echten Polynombruch. Hier ein Beispiel:
Bei der Division vom Polynomen gibt es auch diese zwei Fälle.
Unser erstes Beispiel einer Polynomdivisionen ging glatt auf:
(x2 -1) : (x+1) = (x-1)
Meist jedoch ergibt eine Polynomdivision ein Polynom q(x)
plus einem echten Polynombruch. Hier ein Beispiel:
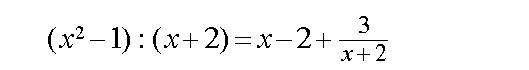 Das Ergebnis kann man übrigens überprüfen, indem man
beide Seiten mit (x+2) multipliziert, jedoch geht es uns
hier erstmal nur um den Satz:
Das Ergebnis kann man übrigens überprüfen, indem man
beide Seiten mit (x+2) multipliziert, jedoch geht es uns
hier erstmal nur um den Satz: