Polynomdivision
durch einen
Linearfaktor
mit dem Hornerschema |
 |
Einleitung |
|
Im folgenden geht es um die
Polynomdivisionen, bei denen
durch Terme der Form (x–a) geteilt wird. Man nennt (x–a) einen
Linearfaktor, weil x nur in der 1.Potenz (d.h. linear) auftritt.
Solche Polynomdivisionen sind besonders einfach durchzuführen,
da man sie mit dem Horner-Schema lösen kann:
Nehmen wir an, wir wollen ein Polynom p(x)
durch einen durch einen Linearfaktor (x-a) teilen:
p(x) : (x–a) = q(x) +r
Gesucht sind also r und die Koeffizienten von q(x) .
Man erhält sie, indem man das HornerSchema für
p(x) an der Stelle a aufstellt:
Die Koeffizienten von q(x) sind die Zahlen in
der unteren Reihe des Horner-Schemas.
r ist gleich der letzten Zahl der unteren Reihe
des Horner-Schemas. |
|
 |
Beispiel |
|
Als Beispiel für eine
"Polynomdivision durch einen
Linearfaktor" wählen wir:
(2x3–3x2+4x-1) : (x+2) =
Wer nun meint (x+2) sei kein Linearfaktor weil vor der 2 kein
Minus steht, der bedenkte das folgender Term gleichwertig ist:
(2x3–3x2+4x–1) : (x–(–2))
=
Der Satz sagt nun, man muß das Horner Schema für
(2x3–3x2+4x–1) an der
Stelle –2 aufstellen:
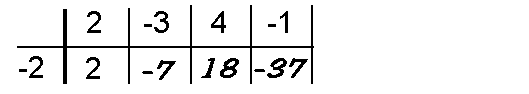
Weiter sagt der Satz: Die untere Reihe entspricht den Koeffizienten
des Ergebnisses q(x), wobei die letzte Zahl (–37) der Rest r ist:
(2x3–3x2+4x–1)
: (x+2) = 2x2–7x+18 Rest –37
|
|