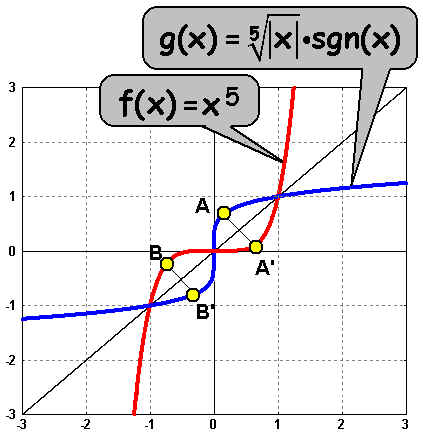
Nun betrachten wir Potenzfunktionen mit  ungeraden Exponenten, im Bsp. f(x)=x⁵.
Da solche Funktionen streng monoton steigend sind, haben sie eine Umkehrfunktion.
Wir wollen die Umkehrfunktion nach der schon bekannten Methode herleiten, d.h.
wir spiegeln den Graphen der Potenzfunktion (rot) an der Winkelhalbierenden
des 1. und 3. Quadranten (schwarze Linie). Aus Punkt A wird A', aus B wird B' usw.
Wir erhalten eine (blaue) Funktion g(x), und stellen anhand des Funktionsgraphen fest:

     Eine Potenzfunktion f(x) mit ungeraden Exponenten
     hat eine Umkehrfunktion g(x)

Beweis anhand Anschauung: Man erkennt das der gespiegelte (blaue) Graph g(x)
eine Umkehrfunktion (und nicht nur eine Umkehrrelation) ist, weil jedem
x-Wert des Definitionsbereichs genau ein Funktionswert  zugeordnet wird.

Übrigens:
Die komische Funtionsgleichung der Umkehrfunktion g(x) erklären wir,
wenn wir die Umkehrfunktion auf der nächsten Seite rechnerisch herleiten.