Auf der vorigen Seite haben wir folgende Potenzfunktion betrachtet:

Als Umkehrung hatten wir die folgende Funktion ermittelt:


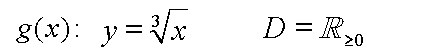
Nun müssen wir noch Schritt 4 durchführen: Überprüfen des Definitions-
bereiches der Umkehrfunktion g(x). Dabei ergibt sich ein Widerspruch:

   Der Definitionsbereich einer Umkehrfunktion ist immer gleich dem
   Wertebereich der ursprünglichen Funktion, müßte also gleich R.

   Die Umkehrfunktion (im Bild blau) die wir ermittelt haben, ist aber
   eine Wurzelfunktion ist, und Wurzelfunktionen haben nur einen
   eingeschränkten Definitionsbereich, nämlich die nicht-negativen
   reellen Zahlen.

Anscheinend ist bei der Berechnung der Umkehrung (Wurzel ziehen=Schritt 3)
der halbe Definitonsbereich und damit die halbe Umkehrfunktion verloren gegangen.
Man sieht dies auch im Bild: Es gibt Punkte der Funktion f(x), wie z.B. den Punkt P,
die keinen gespiegelten Punkt auf g(x) haben:



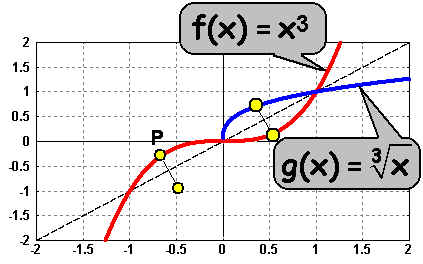
Man kann sich helfen, indem man den restlichen Teil der Umkehrfunktion
sozusagen "von Hand" hinzufügt. Dies geht durch folgende Fallunterscheidung:

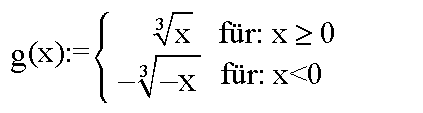
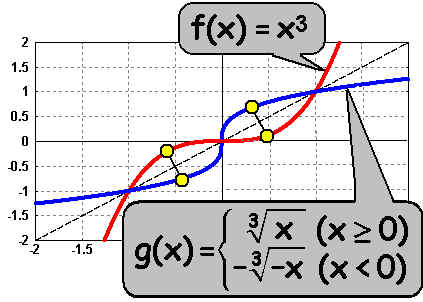
Nun haben wir die vollständige Umkehrfunktion gefunden. Man sieht
dies auch am Graphen, denn die rechnerische Lösung stimmt nun mit
der zeichnerischen Lösung (Spiegelung) überein.

 

Nun haben wir die Umkehrfunktion g(x) gefunden. Manchmal stört jedoch
die Fallunterscheidung bei g(x), z.B. wenn man die Umkehrfunktion von
einem Funktionsplotter ausdrucken lassen will. Um zu einen geschlossenen
Ausdruck (d.h. einer Funktionsgleichung ohne Fallunterscheidung) für die
Umkehrfunktion g(x) zu erhalten, kann man die Signumfunktion (Vorzeichen-
funktion) in Kombination mit dem Betragszeichen benutzen:


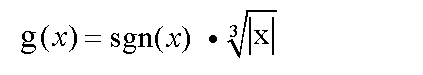
Die sgn-Funktion hat den Funktionswert 1 für positive x (und die Null)
und den Funktionswert –1 für negative x. Das sgn-Zeichen ersetzt also
das Minuszeichen vor der Wurzel, während das Betragszeichen das
Minuszeichen im Radikanten ersetzt.