Die Umkehrung von Potenzfunktionen mit ungeraden Exponenten, z.B.

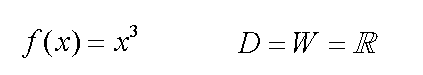
wird in Büchern meist nicht betrachtet, um die soeben geschilderte
Fallunterscheidung zu kompliziert ist.

Stattdessen wird der Definitionsbereich willkürlich eingeschränkt

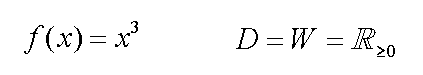
Die Umkehrfunktion lautet dann:

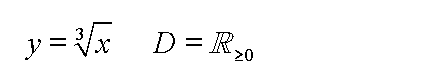
Auf diese Weise, wurde das Problem umgangen.

Eine andere Art das Problem zu umgehen ist folgende: Man fragt nicht
nach der Umkehrfunktion der ungeraden Potenzfunktion, sondern nach
der Umkehrfunktion der ungeraden Wurzelfunktion (ungerader Exponent).
Als Umkehrfunktion erhält man die Potenzfunktion, wobei der
Definitionsbereich gleich den nicht-negativen Zahlen ist. Grund:
Die Wurzelfunktion einen nicht-negativen Wertebereich hat, und dieser muß
laut Vorschrift der Definitonsbereich der Umkehrfunktion (Potenzfunktion) sein.
  

Viele Bücher^* (besonders alte) geben als Umkehrfunktion der ungeraden Potenzfunktion:

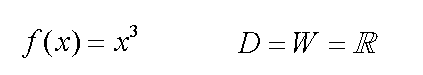
die ungerade Wurzelfunktion an (man beachte den Definitionsbereich):

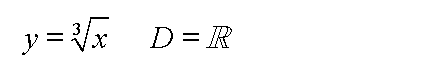
Dies ist nach heutiger Sichtweise falsch, denn die Wurzelfunktion ist nur
für nicht-negative x definiert (d.h. für R₊), genauso wie die Wurzel selbst
(siehe Kurs Wurzelrechnung).

^* Falsch z.B. bei folgenden Standardwerken:
   Dörsam: Mathematik verständlich erklärt
   Kusch/Jung: Funktionen und Differentialrechnung
   Larson: Precalculus
   Kreul/Leupold: Lehrgang der Elementarmathematik

   Richtig z.B. bei folgenden Standardwerken:
   Schäfer/Georgi/Trippler: Vorkurs Mathematik