Betragsgleichungen
der Form |x+a|=c
|
 |
Die Betragsgleichung |x+a|=c |
|
Nun wollen wir uns überlegen, wie man
Betragsgleichungen löst,
die folgende Form haben:

Auch hier müssen wir drei Fälle unterscheiden: |
 |
Fall 1: c ist positiv |
|
Die Betragsgleichung hat dann zwei
Lösungen:
Die erste Lösung ergibt sich, wenn der Term im Betragszeichen
(also x+a) gleich c wird, denn dann gilt: |c| = c und somit:
c=c
Wir halten fest: x+a = c ergibt eine
Lösung der Betragsgleichung
Die zweite Lösung ergibt sich, wenn der Term im Betragszeichen
(also x+a) gleich –c wird, denn dann gilt: |–c| = c und
somit: c=c
Wir halten fest: x+a = –c ergibt eine
Lösung der Betragsgleichung
Zusammengefaßt ergeben sich die beiden Lösungen aus:
x+a = ±c
Wir stellen die Formel um, und erhalten die Lösungen der Betragsgleichung:
x = –a±c |
 |
Fall 2: c ist gleich Null |
|
Wir untersuchen also den Fall: |x+a|=0
In diesem Fall hat die Gleichung nur eine Lösung, nämlich –a,
denn nur wenn x=a gilt, ist die Betragsgleichung wahr:
|–a+a|=0
<=> |0|=0
<=> 0=0 |
 |
Fall 3: c ist negativ |
|
Als Beispiel betrachten wir die Gleichung:
|x–a| = –7
Die linke Seite ist auf jeden Fall positiv (wegen den Betragszeichen),
die rechte Seite der Gleichugn ist negativ. Die Gleichung ist also stets
unwahr, d.h. die Gleichung hat keine Lösung. |
 |
Zusammenfassung der Fälle |
|
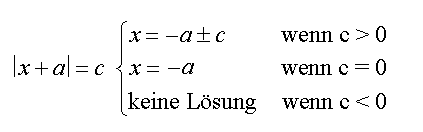 |
|