|
Satz über das Vorzeichen eines Bruches |
 |
Vorwort |
|
Grundlage des in diesem Kapitel vorgestellen Lösungsverfahrens ist
der
Satz über das Vorzeichen eines Bruches:
|
 |
Satz |
|
Grundlage des in diesem Kapitel vorgestellen Lösungsverfahrens ist
der
Satz über das Vorzeichen eines Bruches:
1. Ein Bruch ist größer Null, wenn
Zähler und Nenner beide positiv sind, oder wenn beide negativ
sind.
2. Ein Bruch ist kleiner Null, wenn Zähler und Nenner
verschiedene Vorzeichen haben.
3. Ein Bruch ist gleich Null, wenn der Zähler gleich Null und
der Nenner ungleich Null ist. |
|
 |
Erklärung von Teil 1 des
Satzes |
|
Nehmen wir an, der Zähler und der Nenner eines Bruches seien beide
positiv, z.B.:
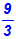
Wir wissen, dass der Bruchstrich ja nur eine andere Schreibweise für
eine Division ist.
Dividiert man aber eine positive Zahl (9) durch eine positive Zahl (3),
so erhält man eine positive Zahl.
Das gleiche gilt, wenn man eine negative Zahl (–8) durch eine negative
Zahl (–4) teilt:
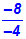
Dividiert man aber eine negative Zahl (–8) durch eine negative Zahl
(–4),
so erhält man eine positive Zahl.
|
 |
Erklärung von Teil 2 des
Satzes |
|
Nehmen wir an, der Zähler und der Nenner eines Bruches haben
unterschiedliche Vorzeichen:
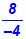
Dividiert man aber eine positive Zahl (8) durch eine negative Zahl (–4),
so erhält man eine negative Zahl.
Wenn man eine negative Zahl durch eine positive dividiert, erhält man
ebenfalls
eine negative Zahl. |
 |
Erklärung von Teil 3 |
|
Ein Bruch ist genau dann gleich Null, wenn der Zähler gleich Null
ist, und der Nenner
ungleich Null ist:
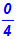
Das der Nenner ungleich Null sein muß, liegt daran, dass die Division
durch Null bekanntlich nicht definiert ist.
|
|