Version 2 ©Raddy1999	Inhalt: Determinanten I zurück
INFO's	Vorkenntnisse: .... Themen: ...... Infos: www.mathematik.net
Was ist eine Determinante	Die Determinantenfunktion ist eine Funktion, die einer quadratischen Matrix eine Zahl (die sogenannte Determinante) zuordnet.
Zweireihige Determinanten	Die Determinantenfunktion ordnet einer zweireihigen Matrix A die Zahl (Determinante) a₁₁a₂₂ – a₂₁a₁₂ zu: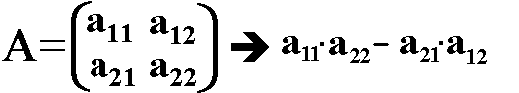
Schreibweisen	Die einer Matrix A zugeordnete Determinante D bezeichnet man oft als: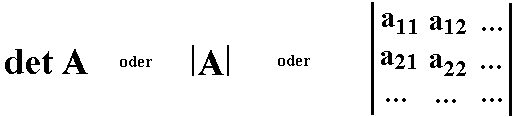
Dreireihige Determinanten	Die Determinantenfunktion ordnet auch einer dreireihigen Matrix A eine Zahl (Determinante) zu. Der Wert dieser Zahl, die \|A\| oder auch D genannt wird, wird durch untenstehende Formel definiert: 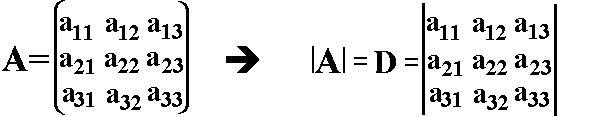\|A\|=a₁₁a₂₂a₃₃+a₁₂a₂₃a₃₁+a₁₃a₂₁a₃₂-a₃₁a₂₂a₁₃-a₃₂a₂₃a₁₁-a₃₃a₂₁a₁₂
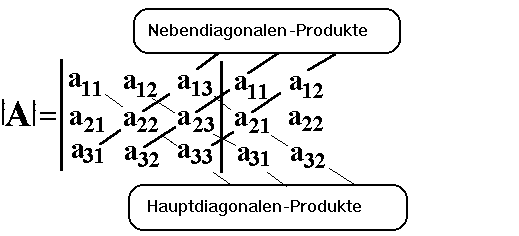
Die Regel von Sarrus	Für die eben genannte lange Formel gibt es eine Merkhilfe (Sarrus-Regel): Hauptdiagonalenprodukte addieren, Nebendiagonalenprodukte subtrahieren:
Beispiel dazu	Berechnung einer dreireihigen Determinante mit der Sarrus-Regel
Determinanten mit >3 Reihen	Werden mit Verfahren gelöst, die in Determinanten II und III näher erläutert werden. Oft auch mit Computerprogrammen.