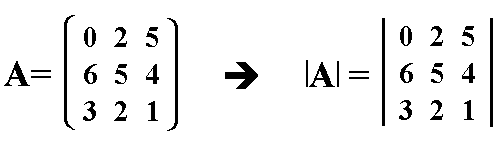| Version
2 ©Raddy 99 |
Determinanten I zurück |
Dreireihige Determinanten |
Als Beispiel sei folgende Matrix gegeben:
Will man nun die Determinante berechnen, so muß man
die obrige Definition benutzen:
|A| = 0·5·1 + 2·4·3 + 5·6·2 – 3·5·5 – 2·4·0 – 1·6·2 = 0+24+60–75–0–12 =–3
Die Determinante |A| hat also den Wert -3.
|
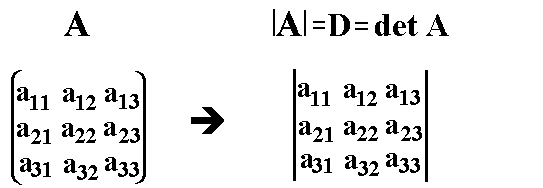 mit |A| = a11a22a33 + a12a23a31 + a13a21a32 – a31a22a13 – a32a23a11 – a33a21a12
mit |A| = a11a22a33 + a12a23a31 + a13a21a32 – a31a22a13 – a32a23a11 – a33a21a12
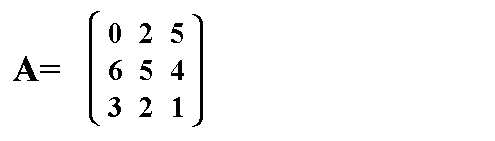 Die Determinantenfunktion ordnet der Matrix A die
Determinante |A| zu:
Die Determinantenfunktion ordnet der Matrix A die
Determinante |A| zu: