 Was ist die Sarrus-Regel
Die auf der vorigen Seite gelernte Definition für
3-reihige Determinanten kann man sich mit der
Regel von Sarrus merken. Sie ist also keine neue
Definition, sondern eine simple Merkhilfe. Was ist die Sarrus-Regel
Die auf der vorigen Seite gelernte Definition für
3-reihige Determinanten kann man sich mit der
Regel von Sarrus merken. Sie ist also keine neue
Definition, sondern eine simple Merkhilfe.
 Erklärung der Regel
Zuerst schreiben wir die zwei ersten Spalten der
Determinante |A| nochmals rechts neben dieselbe: Erklärung der Regel
Zuerst schreiben wir die zwei ersten Spalten der
Determinante |A| nochmals rechts neben dieselbe:
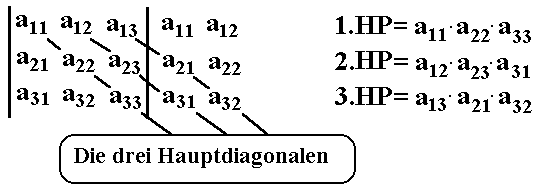
 Die drei im folgenden Bild eingezeichneten Diagonalen
nennt man die Hauptdiagonalen. Das Produkte je einer
Hauptdiagonalen nennt man Hauptdiagonalenprodukt.
Wir haben also drei Hauptdiagonalenprodukte (kurz HP's):
Die drei im folgenden Bild eingezeichneten Diagonalen
nennt man die Hauptdiagonalen. Das Produkte je einer
Hauptdiagonalen nennt man Hauptdiagonalenprodukt.
Wir haben also drei Hauptdiagonalenprodukte (kurz HP's):
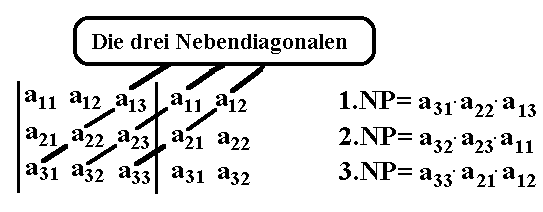
 Die anderen drei Diagonalen nennt man Nebendiagonalen
bzw. ihre Produkte die Nebendiagonalen-Produkte.
Die anderen drei Diagonalen nennt man Nebendiagonalen
bzw. ihre Produkte die Nebendiagonalen-Produkte.
 Addiert man die drei Hauptdiagonalen-Produkte und
subtrahiert davon die drei Nebendiagonalen-Produkte,
so erhält man die von der Vorseite bekannte Formel für |A|:
|A|=a11a22a33+a12a23a31+a13a21a32-a31a22a13-a32a23a11-a33a21a12
Addiert man die drei Hauptdiagonalen-Produkte und
subtrahiert davon die drei Nebendiagonalen-Produkte,
so erhält man die von der Vorseite bekannte Formel für |A|:
|A|=a11a22a33+a12a23a31+a13a21a32-a31a22a13-a32a23a11-a33a21a12
|