Deteminanten 2 - Inhalt (22k2s0)

Version 1 ©Raddy '99	Inhalt: Determinanten II zurück
Info-Seite	Vorkenntnisse: .... Themen: ...... Infos: www.mathematik.net
Einreihige Determinante	Eine 1-reihige Determinante hat den gleichen Wert wie ihr (einzige) Element: \|a₁₁\|= a₁₁
Schnittpunkt- element	Streicht man in einer n-reihigen Determinante eine beliebige Zeile i sowie zusätzlich eine beliebige Spalte k, so nennt man das Element a_ik das Schnittpunktelement.
Unterdeterminante	Streicht man in einer n-reihigen Determinante eine beliebige Zeile i sowie zusätzlich eine beliebige Spalte k, so bilden die übriggebliebenen Elemente die sogenannte 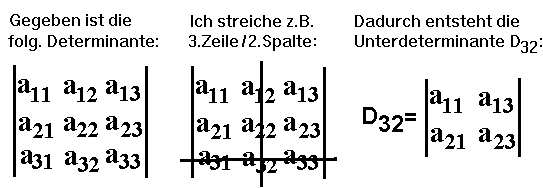Unterdeterminante D_ik :
Vorzeichenfaktor	Die Vorzeichenfunktion ordnet Unterdeterminanten ein Vorzeichen zu: D_ik v_ik = (-1)^i+k
Entwicklungsformel	Man kann in einer Definition festlegen, wie man eine Determinante durch ihre Unterdeterminanten D_ik ausdrückt: Gegeben sei eine n-reihige Determinante. Ich schreibe die Determinante n-mal auf. Dann streiche ich in allen Determinanten die erste Zeile und zusätzlich in der n-ten Determinante die n-te Spalte. Ich addiere die entstandenen Unterdeterminanten und multipliziere sie mit dem gleichnamigen Vorzeichenfaktor und Schnittpunktelement: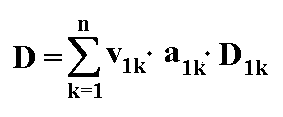
Beispiel	Umwandlung 3-reihige Determinante in 2-reihige Determinanten.
Folgerung	Durch wiederholtes Anwenden der Entwicklungsformel kann man jede n-reihige Determinante durch 1-reihige Determinanten ausdrücken.
Beispiel	Umwandlung einer 3-reihigen Determinante in einreihige Determinanten.
Definition	Die Determinantenfunktion kann man folgendermaßen definieren: Man definiert, wie man 1-reihige Determinanten berechnet (haben wir zu Beginn des Kapitels gemacht). Man definiert, wie man eine beliebige Determinante durch 1-reihige Determinanten ausdrückt (haben wir definiert, indem wir die Entwicklungsformel definierten).
Beispiel	Berechnung einer 3-reihigen Determinante mit dieser Definition.