Entwicklungsformel
|
 Vorbemerkung
Jetzt definieren wir eine n-reihige Determinante durch ihre Unterdeterminanten.
Die Formel nennen wir Entwicklungsformel. Auf den nächsten Seiten werden
wir dann sehen, wozu diese Formel zu gebrauchen ist. Vorbemerkung
Jetzt definieren wir eine n-reihige Determinante durch ihre Unterdeterminanten.
Die Formel nennen wir Entwicklungsformel. Auf den nächsten Seiten werden
wir dann sehen, wozu diese Formel zu gebrauchen ist.
 Definition der Entwicklungsformel Definition der Entwicklungsformel
 Gegeben sei eine n-reihige-Determinante, im Beispiel eine 3-reihige: Gegeben sei eine n-reihige-Determinante, im Beispiel eine 3-reihige:
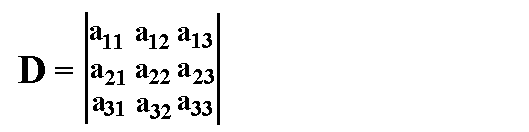
 Hat die Determinante n-Reihen, so schreiben wir sie n-mal
nebeneinander, d.h. in unserem Beispiel 3-mal: Hat die Determinante n-Reihen, so schreiben wir sie n-mal
nebeneinander, d.h. in unserem Beispiel 3-mal:
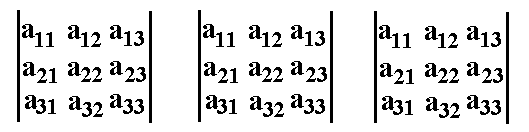
 Nun streichen wir in allen Determinanten die erste Reihe, sowie
in der n-ten Determinante die n-te Spalte: Nun streichen wir in allen Determinanten die erste Reihe, sowie
in der n-ten Determinante die n-te Spalte:
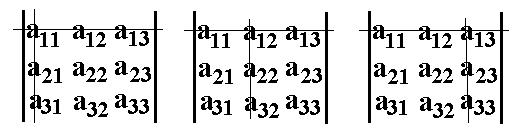
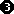 Es entstehen n Unterdeterminanten (im Beispiel entstehen drei): Es entstehen n Unterdeterminanten (im Beispiel entstehen drei):
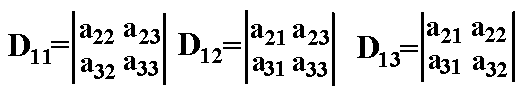
 Diese Unterdeterminanten addieren wir: D11+D12+D13+...+D1n Diese Unterdeterminanten addieren wir: D11+D12+D13+...+D1n
 Jetzt multiplizieren wir noch jede Unterdeterminante mit dem
gleichnamigen Vorzeichenfaktor und Schnittpunkt-Element:
V11a11D11 + V12a12D12 + ... + V1na1nD1n Jetzt multiplizieren wir noch jede Unterdeterminante mit dem
gleichnamigen Vorzeichenfaktor und Schnittpunkt-Element:
V11a11D11 + V12a12D12 + ... + V1na1nD1n
 Schließlich definieren wir, daß diese Formel gleich der
gegebenen Determinante D sein soll:
D = V11a11D11 + V12a12D12 + ... + V1na1nD1n
Meist schreibt man die Enwicklungsformel mit dem Schließlich definieren wir, daß diese Formel gleich der
gegebenen Determinante D sein soll:
D = V11a11D11 + V12a12D12 + ... + V1na1nD1n
Meist schreibt man die Enwicklungsformel mit dem 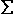 -Zeichen: -Zeichen:
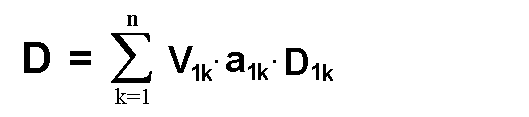
|