Folgerung aus der
Entwicklungsformel
|
 Vorbemerkung
Die letzte Definition (Entwicklungsformel) definierte eine
Determinante durch ihre Unterdeterminanten. Sehr wichtig
ist folgende Folgerung, die sich aus dieser Definition ergibt:
Folgerung
Durch mehrfaches Anwenden
der
Entwicklungsformel kann man jede
Determinante D durch einreihige
Determinanten ausdrücken |
Prinzipielles Vorgehen
Nehmen wir an, wir haben eine 10-reihige Determinante.
Wenden wir auf sie die Entwicklungsformel an, so erhalten
wir eine Formel mit 9-reihigen Determinanten.
Wenden wir auf jede dieser 9-reihigen Determinanten nun
wiederum die Entwicklungsformel an, so erhalten wir eine
Formel mit 8-reihigen Determinanten.
Führt man dieses Verfahren fort, so gelangt man zu einem Term,
in dem alle vorkommenden Determinanten einreihig sind.
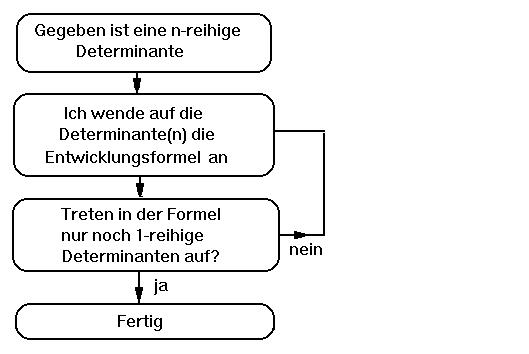
Das Bild zeigt, wie man Vorgehen muß:
Ausführliches Beispiel
Ein ausführliches Beispiel folgt auf der nächsten Seite.
|