 Vorbemerkung
Im letzten Kapitel definierten wir die Determinantenfunktion.
Mit dieser Definition kann man jede Determinante berechnen.
Es gibt aber noch andere Definitionen der Determinantenfunktion,
z.B. die Laplace'sche Definition (oft Laplace'scher Entwicklungssatz
genannt). Mit dieser Laplace'schen Definition kann man die meisten
Determinanten leichter berechnen, als mit der "alten" Definition. Vorbemerkung
Im letzten Kapitel definierten wir die Determinantenfunktion.
Mit dieser Definition kann man jede Determinante berechnen.
Es gibt aber noch andere Definitionen der Determinantenfunktion,
z.B. die Laplace'sche Definition (oft Laplace'scher Entwicklungssatz
genannt). Mit dieser Laplace'schen Definition kann man die meisten
Determinanten leichter berechnen, als mit der "alten" Definition.
 Die Laplace'sche Definition
Zuerst wiederholen wir die "alte" Definition. Sie besteht aus
zwei Teilen:
- Definition 1-reihiger Determinanten
- Entwicklungsformel
Wir wollen die beiden Teile der Defintion kurz wiederholen: Die Laplace'sche Definition
Zuerst wiederholen wir die "alte" Definition. Sie besteht aus
zwei Teilen:
- Definition 1-reihiger Determinanten
- Entwicklungsformel
Wir wollen die beiden Teile der Defintion kurz wiederholen:
Definition einreihiger Determinanten: |a11| = a11
Entwicklungsformel:
 Gegeben sie eine n-reihige Determinante Gegeben sie eine n-reihige Determinante
 Wir schreiben die Determinante n-mal nebeneinander. Wir schreiben die Determinante n-mal nebeneinander.
 Wir streichen in allen Determinanten die erste Zeile und
zusätzlich in der n-ten Determinante die n-te Spalte. Wir streichen in allen Determinanten die erste Zeile und
zusätzlich in der n-ten Determinante die n-te Spalte.
 Wir addieren die entstandenen Unterdeterminanten. Wir addieren die entstandenen Unterdeterminanten.
 Jede der Unterdeterminanten multiplizieren wir mit dem
gleichnamigen Schnittpunktelement und Vorzeichenfaktor.
Nun zur Laplace'schen Definition. Sie unterscheidet sich von der
"alten" Definition nur dadurch, daß Punkt Jede der Unterdeterminanten multiplizieren wir mit dem
gleichnamigen Schnittpunktelement und Vorzeichenfaktor.
Nun zur Laplace'schen Definition. Sie unterscheidet sich von der
"alten" Definition nur dadurch, daß Punkt 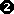 etwas anders lautet: etwas anders lautet:
 Wir wählen eine beliebige Zeile (bzw. Spalte) aus, und
streichen sie in allen Determinanten. Zusätzlich streichen wir
in der n-ten Determinante die n-te Spalte (bzw. n-te Zeile).
Prinzipiell darf man hier eine beliebige Zeile oder Spalte wählen,
doch am schnellsten und leichtesten läßt sich die Determinante lösen,
wenn man diejenige Zeile oder Spalte wählt, in der die meisten
"Nullen" stehen. Das Beispiel auf der folgenden Seite zeigt dies. Wir wählen eine beliebige Zeile (bzw. Spalte) aus, und
streichen sie in allen Determinanten. Zusätzlich streichen wir
in der n-ten Determinante die n-te Spalte (bzw. n-te Zeile).
Prinzipiell darf man hier eine beliebige Zeile oder Spalte wählen,
doch am schnellsten und leichtesten läßt sich die Determinante lösen,
wenn man diejenige Zeile oder Spalte wählt, in der die meisten
"Nullen" stehen. Das Beispiel auf der folgenden Seite zeigt dies.
 Sprechweise
Der Punkt Sprechweise
Der Punkt 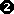 der Laplace'schen Definition lautete:
Wir wählen eine beliebige Zeile oder Spalte ....
Wählt man hier z.B. die dritte Spalte, so sagt man:
Wir entwickeln die Determinante nach der dritten Spalte. der Laplace'schen Definition lautete:
Wir wählen eine beliebige Zeile oder Spalte ....
Wählt man hier z.B. die dritte Spalte, so sagt man:
Wir entwickeln die Determinante nach der dritten Spalte.
|