Die Laplace'sche Definition als Formel
Wir sagten, daß sich "alte" und "neue" Definiton nur dadurch
unterscheiden, daß die Entwicklungsformel etwas anders lautet:
Die alte Entwicklungsformel lautete:
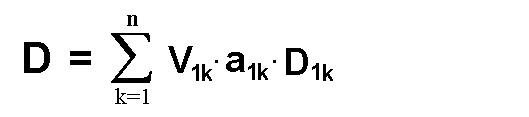Die neue Entwicklungsformel besteht aus zwei Varianten,
je nachdem, ob man (in Schritt 2 der Entwicklungsformel)
eine Zeile oder eine Spalte streichen möchte:
Anmerkung
Eigentlich müßte man jetzt beweisen, daß die "alte" Definition und
die "neue" Definition (Laplace'sche Definition) gleich sind, denn man
kann ein mathematisches Objekt nicht zweimal definieren. Dies wäre
so, als wenn man einem Kind zwei verschiedene Namen geben würde.
Den Beweis verschieben wir aber auf ein späteres Kapitel.
Die Laplace'sche Definition als Formel
Wir sagten, daß sich "alte" und "neue" Definiton nur dadurch
unterscheiden, daß die Entwicklungsformel etwas anders lautet:
Die alte Entwicklungsformel lautete:
Die neue Entwicklungsformel besteht aus zwei Varianten,
je nachdem, ob man (in Schritt 2 der Entwicklungsformel)
eine Zeile oder eine Spalte streichen möchte:
