Beispiel zum
Laplace'schen
Entwicklungssatz
|
 Beispiel zum Laplace'schen Entwicklungssatz
Gegeben sei folgende Determinante: Beispiel zum Laplace'schen Entwicklungssatz
Gegeben sei folgende Determinante:
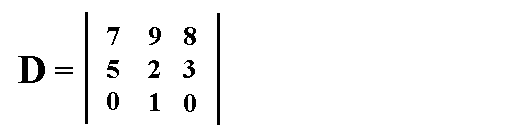 Laut Punkt 1 der Definition wird die Determinante 3x aufgeschrieben:
Laut Punkt 1 der Definition wird die Determinante 3x aufgeschrieben:
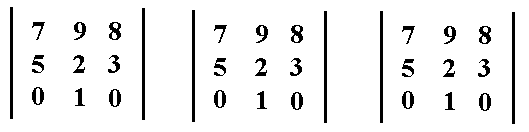 Laut Punkt 2 der Definition müssen wir wahlweise eine Zeile oder
eine Spalte streichen, und zusätzlich in der n-ten Determinante die
n-te Spalte bzw. Zeile.
Wie gesagt ist es am einfachsten nach derjenigen Zeile oder Spalte
zu entwickeln, die die meisten "Nullen" enthält. In diesem Beispiel
ist dies die dritte Zeile, also sollten wir die Determinante nach der
dritten Zeile entwickeln:
Laut Punkt 2 der Definition müssen wir wahlweise eine Zeile oder
eine Spalte streichen, und zusätzlich in der n-ten Determinante die
n-te Spalte bzw. Zeile.
Wie gesagt ist es am einfachsten nach derjenigen Zeile oder Spalte
zu entwickeln, die die meisten "Nullen" enthält. In diesem Beispiel
ist dies die dritte Zeile, also sollten wir die Determinante nach der
dritten Zeile entwickeln:
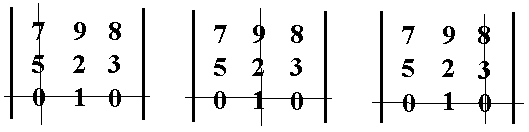 Wir addieren die entstandenen Unterdeterminanten und multiplizieren
sie mit dem gleichnamigen Schnittpunktelement und Vorzeichenfaktor:
Wir addieren die entstandenen Unterdeterminanten und multiplizieren
sie mit dem gleichnamigen Schnittpunktelement und Vorzeichenfaktor:
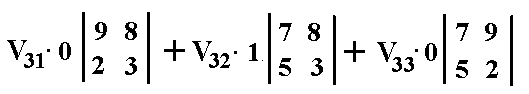 Der 1. und 3. Summand fallen weg. Nun berechnen wir V32:
V32=(-1)3+2 = -1
Jetzt müssen wir nur noch die Unterdeterminante D32 berechnen:
Wir entwickeln sie nach der ersten Zeile, da eine Entwicklung nach
einer anderen Zeile oder Spalte auch keinen Vorteil bringen würde:
Der 1. und 3. Summand fallen weg. Nun berechnen wir V32:
V32=(-1)3+2 = -1
Jetzt müssen wir nur noch die Unterdeterminante D32 berechnen:
Wir entwickeln sie nach der ersten Zeile, da eine Entwicklung nach
einer anderen Zeile oder Spalte auch keinen Vorteil bringen würde:
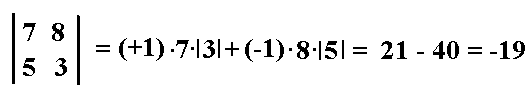 Damit ist die Determinante berechnet:
D = (-1) · 1 · (-19) = 19
Damit ist die Determinante berechnet:
D = (-1) · 1 · (-19) = 19
|