| 1.Beide Seiten sind
positiv: |
Bis jetzt haben wir noch nicht darüber gesprochen, ob man
überhaupt beide Seiten
einer Gleichung logarithmieren darf, ohne das sich die
Lösungsmenge ändert.
Mit anderen Worten: Ist Logarithmieren eine Äquivalenzumformung?
Prinzipiell ist die Rechenoperation "Logarithmieren" eine
Äquivalenzumformung,
solange man nur positive Zahlen logarithmiert, denn es gilt:
| |
Sind zwei positive Zahlen gleich,
dann
sind auch ihre
Logarithmen gleich:
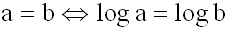 |
|
Solange man nur positive Zahlen logarithmiert, gibt es also
keine Probleme.
Die übrigen zwei nun folgenden Fälle, führen wir auf diesen Fall
zurück.
| 2.Beide Seiten sind
negativ: |
Nun überlegen wir uns, wie wir vorgehen müssen, wenn beide
Seiten einer
Exponentialgleichung negativ sind. Im folgenden Beispiel sind
die Seiten der
Gleichung negativ (Beachte: 2x
ist positiv und somit ist
–2x
auf jeden Fall negativ:
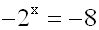
Hier dürfen wir nicht sofort logarithmieren, denn der
Logarithmus aus einer
negativen Zahl ist ja nicht definiert. Es gibt aber eine
einfache Lösung, um
dieses Problem zu umgehen. Wir müssen nur beide Seiten mit
–1 multiplizieren,
und erhalten dadurch eine Exponentialgleichung, bei der beide
Seiten positiv sind:
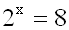
| 3.Eine Seite negativ,
eine Seite unklar: |
In der folgenden Exponentialgleichung ist die rechte
Seite negativ,
das Vorzeichen der linken Seite hängt aber davon ab, ob wir eine
gerade oder eine ungerade Zahl für x einsetzen.
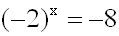
Auch hier darf man nicht logarithmieren, denn wir wissen ja
nicht,
ob die linke Seite positiv oder negativ ist.
Wir müssen hier den gleichen Trick anwenden, den wir schon im
Kurs "Potenzgleichungen" angewendet haben. Wir potenzieren
beide Seiten mit 2. Wir müssen nur beachten, daß wir dann am
Ende der Rechnung die Probe machen müssen, denn Potenzieren
mit einer geraden Zahl ist keine Äquivalenzumformung (es können
Lösunge hinzukommen):
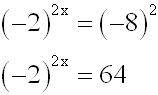
Auf der linken Seite wenden wir nun ein Potenzgesetz an, und
zwar
das Gesetz über die "Potenz einer Potenz":
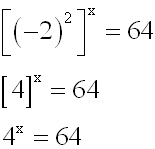
Jetzt haben wir wieder eine Exponentialgleichung, mit 2
positiven Seiten,
die wir durch logarithmieren lössen können. Es ergibt sich die
Lösung:
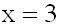
Wie gesagt darf man nicht vergessen, am Ende der Rechnung die
Probe zu machen.
|