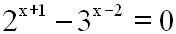
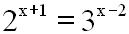
Exponentialgleichungen mit 3 Summanden 1.Exponentialgleichungen mit zwei Summanden (Wiederholung): Bis jetzt haben wir nur Exponentialgleichungen betrachtet, die aus zwei Summanden bestanden: Wir haben dann die zwei Summanden auf  beide Seite verteilt: und die Gleichung dann logarithmiert, wodurch sich die Lösung ergab. 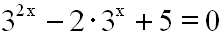2.Exponentialgleichungen mit drei Summanden: Jetzt betrachten wir Exponentialgleichungen mit drei Summanden:         Hier wäre es sinnlos, das Lösungsverfahren "Logarithmieren" anzuwenden, d.h. die Potenzen auf beide Seiten zu verteilen, und danach zu logarithmieren. 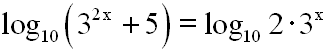Es ergäbe sich die Gleichung: Diese Gleichung kann nicht weiter vereinfacht, und somit ist sie nicht lösbar. Wir sehen, daß der folgende Satz gilt:         Im Allgemeinen sind daher Exponentialgleichungen mit drei      oder mehr Summanden nicht durch Logarithmieren lösbar.    Es gibt aber Sonderfälle die mit Hilfe der sogenannten "Substitution" lösbar sind. 3.Lösen von Exponentialgleichungen mit 3 Summanden: Auf der nächste Seiten werden wir ein neues Lösungsverfahren für Exponentialgleichungen kennenlernen. Es ist die Substitution. Mit ihr kann man zumindest einige Sonderfälle von Exponentialgleichungen lösen, die drei oder mehr Summanden haben.