|
|
|
1.Substitution der gegebenen Gleichung: |
Nun wollen wir das Lösungsverfahren Substitution
erklären.
Gegeben sei die Exponentialgleichung:
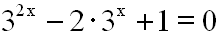
Nun wandeln wir den ersten Summanden der Gleichung mit
Hilfe
eines Potenzgesetzes um:
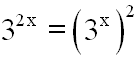
Damit wir die ursprüngliche Gleichung zu:
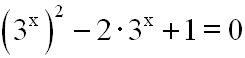
In dieser Gleichung kommt nun zweimal der Ausdruck 3x
vor.
Diesen Ausdruck ersetzen (substituieren) wir nun durch
die neue
Variable, der wir den Namen u.geben. Die Gleichung
lautet nun:
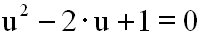
Wir haben also 3x
durch u substituiert, und eine quadratische
Gleichung erhalten.
|
|
2.Die substituierte Gleichung lösen: |
Als nächstes müssen wir die substituierte Gleichung
lösen:
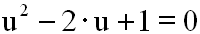
Dazu benutzen wir die bekannte p-q-Lösungsformel:
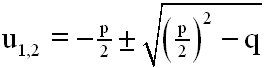
Wir setzen die Koeffizienten der quadratischen Gleichung
in die Lösungsformel ein:
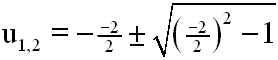
Ausrechnen der Formel ergibt die Lösung:
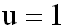
|
| 3.Rücksubstitution
durchführen: |
Im Schritt 1 hatten wir die
Substitution 3x=u
durchgeführt, und dann im Schritt 2 die Variable u
berechnet.
Wir wollen aber nicht u berechnen, sondern x. Daher
müssen wir nun die Substitution rückgängig machen,
d.h. wir müssen u wieder durch 3x
ersetzen:
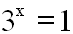
|
| 4.Rücksubstitutierte
Gleichung lösen: |
Jetzt haben wir wieder eine Exponentialgleichung,
aber diese ist viel
einfacher als die gegebene Gleichung. Wir lösen sie
durch logarithmieren:
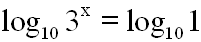
Auf der rechten Seite wenden wir ein Logarithmusgesetz
an:
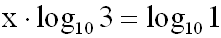
Wir bringen alle Konstanten auf die linke Seite:
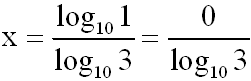
Wir erhalten die Lösung der
Exponentialgleichung:
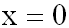 |
|
|