|
|
| 1.Substitution
vorbereiten: Potenzen umformen: |
|
Wir betrachten wieder eine Gleichung mit drei
Summanden:
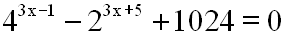
Hier scheint keine Substitution möglich zu sein, denn
weder die Basen noch
die Exponenten sind gleich.Man kann aber die beiden
Basen ineinander umwandeln,
denn die erste Basis (4) ist eine Potenz der zweiten
Basis (2):
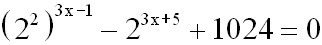
Jetzt müssen wir nur noch das Potenzgesetz für Potenzen
anwenden:
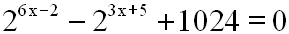
Nun sind nur noch die Exponenten verschieden, doch auch
diese kann man gleich
machen. Dazu wenden wir das Produktgesetz für Potenzen
an:
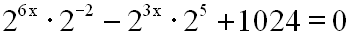
Betrachten wir nun die beiden Exponenten, die die
Unbekannte x enthalten.
Der erste Exponent ist doppelt so groß wie der zweite,
was wir erkennen, wenn
wir die Schreibweise im ersten Exponenten verändern:
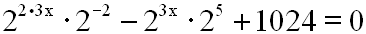
Nun müssen wir auf den ersten Exponenten nochmals das
Potenzgesetz für Potenzen anwenden, und erhalten:
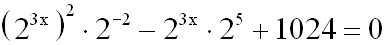
Nun sind die beiden Potenzen mit der Unbekannten gleich,
und
wir können die Substitution durchführen. Allerdings
vereinfachen
wir die Gleichung vorher, indem wir die Konstanten
berechnen:
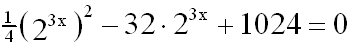
|
|
2.Substitution der gegebenen Gleichung: |
|
Nun können wir die Substitution 23x
= u durchführen:
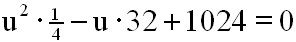
Jetzt multiplizieren wir die Gleichung mit 4, damit der
Bruch verschwindet:
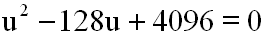
Es liegt nun eine quadratische Gleichung in Normalform
vor.
|
|
3.Die substituierte Gleichung lösen: |
|
Diese substituierte Gleichung lösen wir mit der
p-q-Lösungsformel
für quadratische Gleichungen in Normalform:
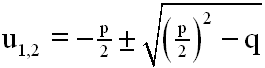
Werte einsetzen:
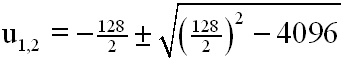
Es ergibt sich die Lösung:

|
| 4.Rücksubstitution
durchführen: |
Wir machen nun die Substitution 23x = u
aus Schritt 2 wieder rückgängig,
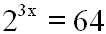 |
| 5.Rücksubstitutierte
Gleichung lösen: |
Die rücksubstituierte Gleichung
lösen wir durch Logarithmieren:
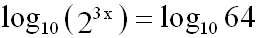
Auf der linken Seite wenden wir das Logarithmusgesetz
für Potenzen an:
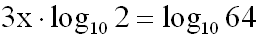
Wir bringen alle Konstanten auf die rechte Seite:
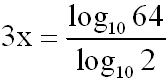
Jetzt müssen wir nur noch die Gleichung
durch 3 teilen:
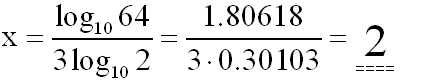
Dies ist die Lösung der
Exponentialgleichung. |
|
|
|
|