Nun wollen wir nochmals zusammenfassen, welche Exponentialgleichungen wir mit Hilfe der
Substitution lösen können.

Eine Exponentialgleichung muß folgende Bedingung erfüllen, damit man sie
mit Hilfe der Substitution in eine algebraische Gleichung umwandeln kann:

   Die Basen aller Potenzen (die die Unbekannte x  im Exponenten haben) müssen
   gleich sein, oder man muß die Basen durch Anwendung der Potenzgesetze
   auf den gleichen Wert bringen können.

Dazu ein Beispiel. In dieser Exponentialgleichung haben alle Basen den gleichen Wert:


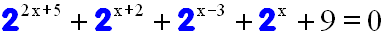
Bei dieser Gleichung sind die Basen zwar nicht gleich, aber man kann sie alle auf einen Wert bringen:


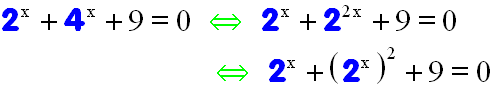
Beim folgenden Beispiel kann man die Basen dagegen nicht gleich machen:


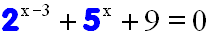
Doch selbst wenn man alle Basen gleich machen kann, und die Substitution somit
durchführbar ist, dann bedeutet dies noch nicht, daß die Exponentialgleichung lösbar ist.

Die Substitution kann nämlich auf eine höhere algebraische Gleichung führen,
wie z.B. ein Gleichung 7.Grades. Da eine solche Algebraische Gleichung im
allgemeinen nicht lösbar ist, ist auch die Exponentialgleichung nicht lösbar.