Version: Test ©Raddy '99
Funktionen I zurück
Vorbemerkung Im Kapitel Relationen II haben wir den Begriff "Funktion" bereits definiert. Zur Erinnerung: Definition
Erläuterungen zur Definition 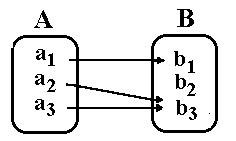Um die Definition zu verdeutlichen benutzen wir das Pfeildiagramm. Eine Funktion ist, wie bereits oben gesagt, eine linksvollständige und rechtseindeutige Relation. Wir müssen daher die Begriffe linksvollständig und rechtseindeutig erklären: Linksvollständigkeit: Die Relation im Bild oben ist linksvollständig, weil bei jedem Element von A ein Pfeil beginnt. Rechtseindeutigkeit: Die Relation im Bild oben ist rechteindeutig, weil die Pfeile (die nach rechts gehen) eindeutig sind, d.h. bei jedem Element von A beginnt höchstens ein Pfeil nach rechts. Der Begriff "Eindeutige Relation" Eine linksvollständige und rechtseindeutige Relation nennt man nun kurz "eindeutig". In dieser Terminologie ist dann eine Funktion eine eindeutige Relation. Schreibweise Für eine Relationen zwischen den Mengen A und B benutzten wir die folgenden Schreibweisen: ARB oder A~B. Für eine Funktion zwischen den Mengen A und B schreibt man dagegen: A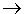B © by www.mathematik.net
Vorbemerkung
Im Kapitel Relationen II haben wir den Begriff "Funktion"
bereits definiert. Zur Erinnerung:
Um die Definition zu verdeutlichen benutzen wir das Pfeildiagramm.
Eine Funktion ist, wie bereits oben gesagt, eine linksvollständige
und rechtseindeutige Relation. Wir müssen daher die Begriffe
linksvollständig und rechtseindeutig erklären:
Linksvollständigkeit:
Die Relation im Bild oben ist linksvollständig, weil
bei jedem Element von A ein Pfeil beginnt.
Rechtseindeutigkeit:
Die Relation im Bild oben ist rechteindeutig, weil die
Pfeile (die nach rechts gehen) eindeutig sind, d.h. bei
jedem Element von A beginnt höchstens ein Pfeil nach rechts.
B
© by www.mathematik.net