Version: Test |
Inhalt zu: Funktionen II zurück |
| Info-Seite | Vorkenntnisse: ... Themen: ... Infos: www.mathematik.net |
| Surjektive Funktion |
Zielmenge B auch zur Wertemenge, so nennt man die Funktion surjektiv. 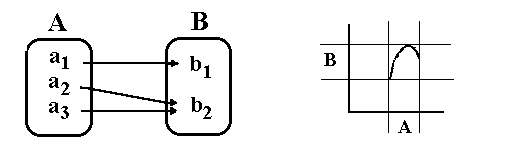 |
| Injektive Funktion |
liegt vor, wenn jedes Element der Zielmenge B höchstens einmal als Bild (eines Elementes der Definitionsmenge) vorkommt. 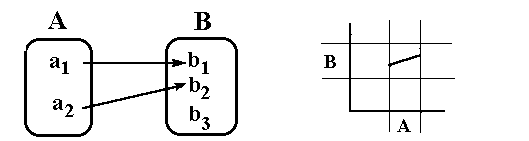 |
| Bijektive Funktion |
Auch genannt: 1.Umkehrbare Funktion 2.Ein-Eindeutige Funktion. daran, daß bei jedem Element der Zielmenge B genau ein Pfeil endet: 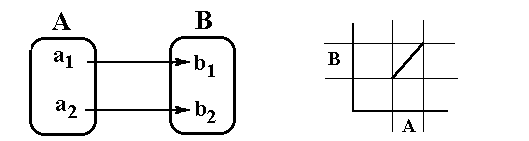 |
| Umkehrrelation | Zu jeder Relation/Funktion existiert eine Umkehrrelation. |
| Umkehrfunktion | Ist die
Umkehrrelation selbst eine Funktion, so nennt man sie Umkehrfunktion. Eine Umkehrfunktion (zu einer Funktion f) existiert genau dann, wenn die Funktion f bijektiv ist. |
| Überblick |
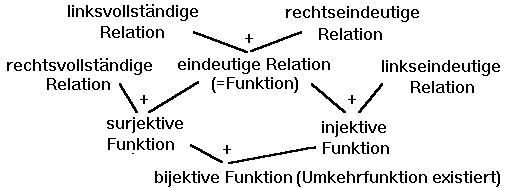 |