Bijektive
Funktion |
 Definition Definition
Man nennt eine Funktion bijektiv
(oder Bijektion), wenn jedes
Element der Zielmenge genau einmal als Bild vorkommt. |
 Alternative Definition Alternative Definition
Man nennt eine Funktion bijektiv
(oder Bijektion),
wenn sie surjektiv und injektiv ist. |
 Beweis der Gleichheit der Definitionen
Nun müssen wir noch beweisen, daß beide Definitionen gleich sind.
Wir beweisen, daß aus der zweiten Definition die erste folgt:
Ist die Funktion surjektiv, dann kommt jedes Element von B
mindestens einmal als Bild vor. Ist die Funktion außerdem injektiv,
so kommt jedes Element von B höchstens einmal als Bild vor.
Kommt jedes Element von B mindestens einmal und gleichzeitig
höchstens einmal als Bild vor, so kommt jedes Element von B
genau einmal als Bild vor. Dies ist aber der Wortlaut der
ersten Definition, wodurch die Gleichheit bewiesen ist. Beweis der Gleichheit der Definitionen
Nun müssen wir noch beweisen, daß beide Definitionen gleich sind.
Wir beweisen, daß aus der zweiten Definition die erste folgt:
Ist die Funktion surjektiv, dann kommt jedes Element von B
mindestens einmal als Bild vor. Ist die Funktion außerdem injektiv,
so kommt jedes Element von B höchstens einmal als Bild vor.
Kommt jedes Element von B mindestens einmal und gleichzeitig
höchstens einmal als Bild vor, so kommt jedes Element von B
genau einmal als Bild vor. Dies ist aber der Wortlaut der
ersten Definition, wodurch die Gleichheit bewiesen ist.
 Pfeildiagramm einer bijektiven Funktion
Im Pfeildiagramm erkennt man die Bijektivität daran, daß bei
jedem Element der Zielmenge genau ein Pfeil endet: Pfeildiagramm einer bijektiven Funktion
Im Pfeildiagramm erkennt man die Bijektivität daran, daß bei
jedem Element der Zielmenge genau ein Pfeil endet:
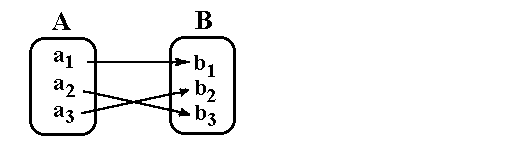
 Graph einer bijektiven Funktion
Bei Funktionen in kartesischen Koordinantensystem erkennt man
Bijektivität daran, daß jedes Element von B als Bild vorkommt,
und die Funktion "streng monton steigend/fallend" ist: Graph einer bijektiven Funktion
Bei Funktionen in kartesischen Koordinantensystem erkennt man
Bijektivität daran, daß jedes Element von B als Bild vorkommt,
und die Funktion "streng monton steigend/fallend" ist:

|