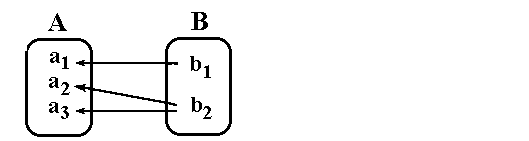 Umkehrrelation zu einer Relation
Um den Begriff Umkehrfunktion zu erklären, wiederholen wir
zunächst an den Begriff Umkehrrelation (Relationen II):
Man bildet die Umkehrrelation einer
Relation,
indem man Vor- und Nachbereich vertauscht |
Wir erinnern uns weiter:
| Zu jeder Relation existiert eine
zugehörige Umkehrrelation. |
Im folgenden Bild zeigt das linke Bild eine Relation und das
rechte Bild die dazugehörige Umkehrrelation:
Umkehrrelation zu einer Funktion
Da nun Funktionen nichts anderes sind als spezielle Relationen
(nämlich eindeutige Relationen), kann man auch zu jeder Funktion
eine Umkehrrelation angeben. Es gilt also folgender Satz:
| Zu jeder Funktion existiert eine
zugehörige Umkehrrelation. |
Ein Beispiel: Gegeben sei die folgende Funktion:
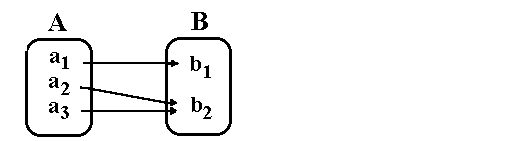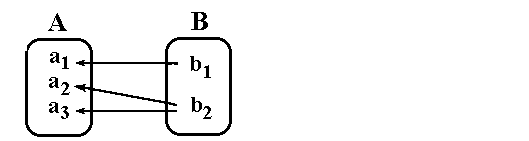
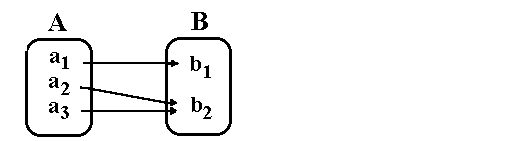Nun vertauschen wir Vor- und Nachbereich, und erhalten
die Umkehrrelation der Funktion:
|