| Umkehrfunktion |
 Umkehrfunktion
Manchmal kommt es vor, daß die Umkehrrelation einer Funktion selbst
wieder eine Funktion ist. In diesem Fall spricht man nicht von einer
Umkehrrelation, sondern von einer Umkehrfunktion. Umkehrfunktion
Manchmal kommt es vor, daß die Umkehrrelation einer Funktion selbst
wieder eine Funktion ist. In diesem Fall spricht man nicht von einer
Umkehrrelation, sondern von einer Umkehrfunktion.
 Beispiel
Gegeben sei die folgende Funktion: Beispiel
Gegeben sei die folgende Funktion:
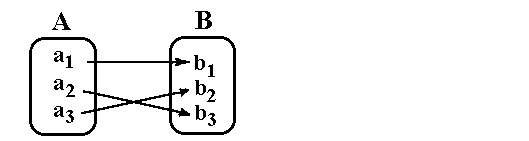 Nun bilden wir die Umkehrrelation dieser Funktion:
Nun bilden wir die Umkehrrelation dieser Funktion:
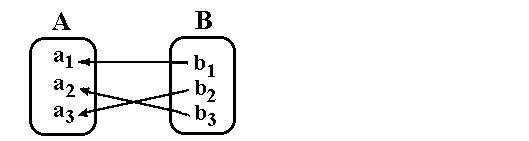 Weil jedem Element von B genau ein Element von A
zugeordnet wird, ist die Umkehrrelation B
Weil jedem Element von B genau ein Element von A
zugeordnet wird, ist die Umkehrrelation B A selbst
eine Funktion, und wird deshalb nicht Umkehrrelation
sondern Umkehrfunktion genannt. A selbst
eine Funktion, und wird deshalb nicht Umkehrrelation
sondern Umkehrfunktion genannt.
 Welche Funktionen haben eine Umkehrfunktion
Nun wollen wir klären, wann eine Funktion eine Umkehrfunktion
besitzt, und wann nur eine Umkehrrelation: Welche Funktionen haben eine Umkehrfunktion
Nun wollen wir klären, wann eine Funktion eine Umkehrfunktion
besitzt, und wann nur eine Umkehrrelation:
Eine Funktion f besitzt genau
dann eine Umkehrfunktion,
wenn die Funktion f eine bijektive Funktion ist. |
Erklärung des Satzes:
Zu einer bijektiven Funktion existiert immer eine Umkehrfunktion.
Zu einer nicht bijektiven Funktion existiert nie eine Umkehrfunktion,
sondern nur eine Umkehrrelation.
|
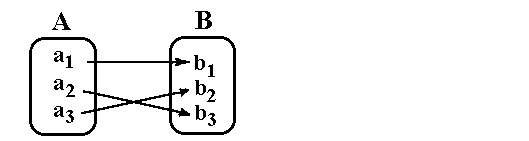 Nun bilden wir die Umkehrrelation dieser Funktion:
Nun bilden wir die Umkehrrelation dieser Funktion:
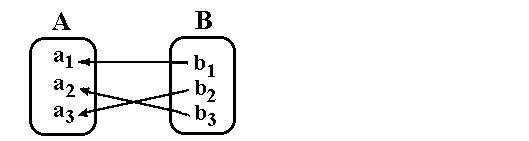 Weil jedem Element von B genau ein Element von A
zugeordnet wird, ist die Umkehrrelation B
Weil jedem Element von B genau ein Element von A
zugeordnet wird, ist die Umkehrrelation B