| Überblick |
 Bild
Erklärung des Bildes
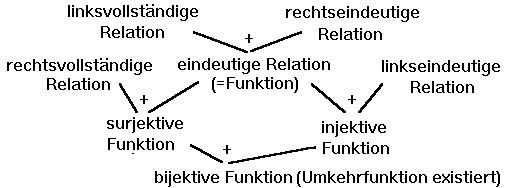
Eine linksvollständige und rechtseindeutige Relation
nennt man eindeutige Relation oder Funktion.
Ist eine Funktion rechtvollständig, so nennt man die
Funktion eine surjektive Funktion.
Ist eine Funktion linkseindeutig, so nennt man die
Funktion eine injektive Funktion.
Ist die Funktion rechtsvollständig und linkseindeutig
(d.h. surjektiv und injektiv), so nennt man die Funktion bijektiv.
Zu bijektiven Funktionen existiert eine Umkehrfunktion,
zu allen anderen Funktionen nur eine Umkehrrelation.
|