Version: Test
©Raddy 2000

Funktionen III                          zurück
Flächen im
Raum		 a-absatz.pcx (280 Byte)Flächen im Raum
       Verbindet man im Beispiel von der Vorseite alle Funktionswerte
       (also alle Punkte) und läßt die Hilfslinien weg, so erhält man als
       Funktionsgraph eine Fläche im Raum. Die Graphen von Funktionen
       zweier Unabhängiger sind also im allgemeinen Flächen: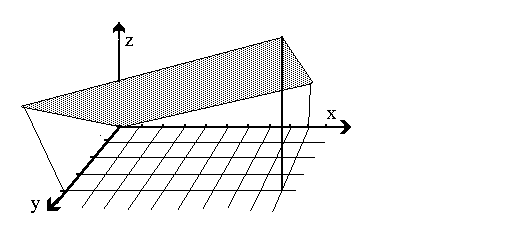
     fu3s2p3.pcx (7041 Byte)
a-absatz.pcx (280 Byte)Zwei weitere Beispiele für Graphen
    von Funktionen zweier Unabhängiger
      Die folgende Bild zeigt ebensfalls einen Funktionsgraphen
      einer "Funktionen zweier unabhängiger Variablen".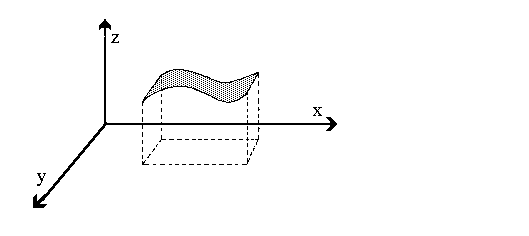
  fu3s3p2.pcx (5144 Byte)
      Als nächstes Beispiel sehen wir den Graph der Halbkugelfunktion.
      Diese Funktion ist ebenfalls die Funktion zweier Unabhängiger.
      Den Funktionsgraphen kann man sich als einen durchgeschnittenen
      Tischtennisball vorstellen (innen hohl):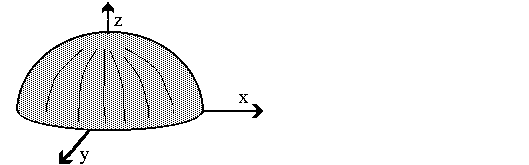

   fu3s3p3.pcx (3265 Byte)

     Der Funktionsgraph dazu lautet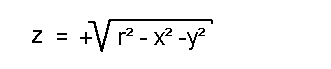
fu3s3p4.pcx (1115 Byte)
      wobei r der Radius der Halbkugel ist.