Version: Test |
Funktionen III zurück |
| Schnitte parallel zur x-z-Ebene (Höhenlinien) |
 BeispielAuf diese Seite wollen wir lernen, wie man die Gleichung eines Schnittes (eine Schnittkurve) berechnet, wenn man eine Fläche parallel zur x-z-Ebene schneidet, wobei die Fläche durch eine "Funktion zweier Unabhängiger" gegeben ist: 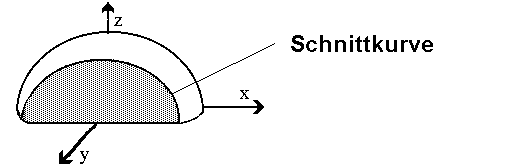 Berechnung der SchnittkurveAls Beispiel wählen wir eine hohle Halbkugel. Die Gleichung der Oberfläche der hohlen Halbkugel lautete: 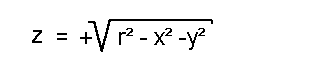 Außerdem soll der Radius der Einfachheit halber 1 sein: 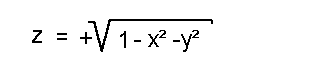 Wie gesagt wollen wir die Halbkugel parallel zur x-z-Ebene scheiden, d.h. wir müssen einen Wert für y wählen, bei dem wir die Fläche schneiden wollen. Wir wählen willkürlich einen Wert von y=0.5: 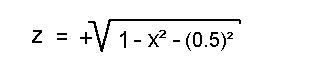 Der Radikant kann vereinfacht werden: 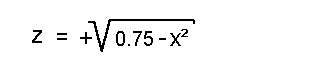 Aus der Geometrie bzw. Kreislehre wissen wir aber, dass dies die Gleichung eines Halbkreises mit dem Radius 0.75 ist. Die Schnittkurve hat also die Form eines Halbkreises mit einem Radius von 0.75. Copyright 2000 by: www.mathematik.net |